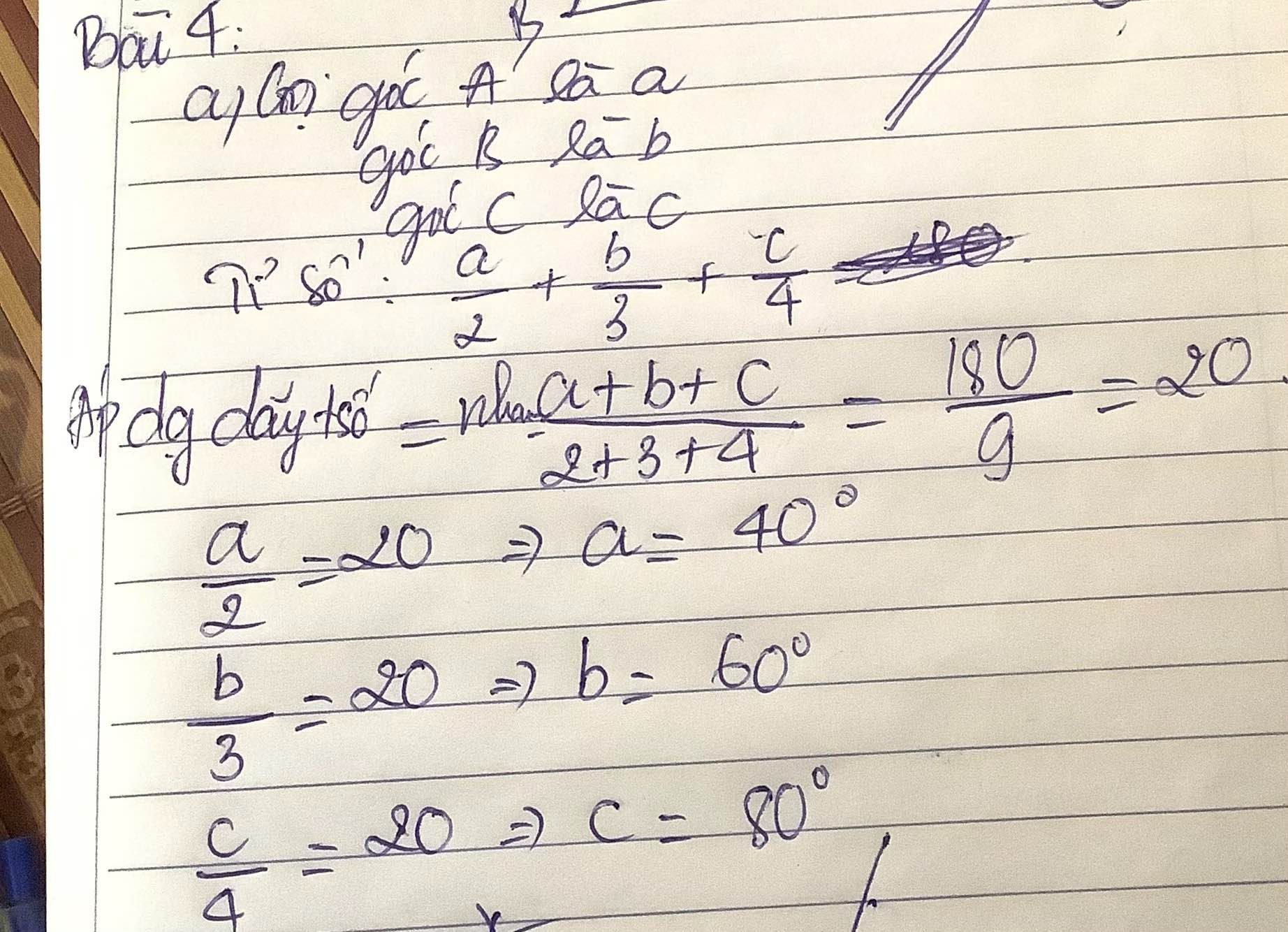Gấp ạ+ vẽ hình
NT
Những câu hỏi liên quan
 vẽ hình ạ làm chi tiết với ạ nhanh gấp
vẽ hình ạ làm chi tiết với ạ nhanh gấp
Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE
Đúng 1
Bình luận (0)
Hãy vẽ lại bản vẽ hình chiếu đứng, hình chiếu cạnh, hình chiếu = của hình chóp nón.
mình đang gấp ạ!!!
Gấp ạ!!! Nãy h ko ai giúp tôi. Vẽ hình nx ạ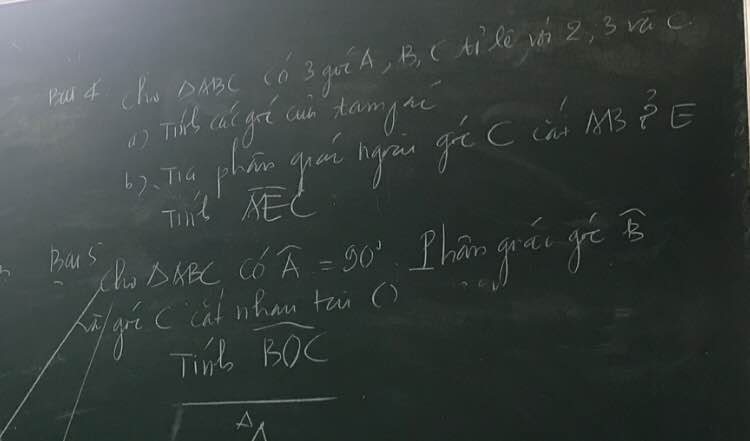
Mk chỉ mới nghĩ ra bài 5 thôi còn dòng đầu bài 4 chữ cuối cùng mk ko biết có phải là"c" ko hay là một con số nữa.
Bài 5 của bạn nè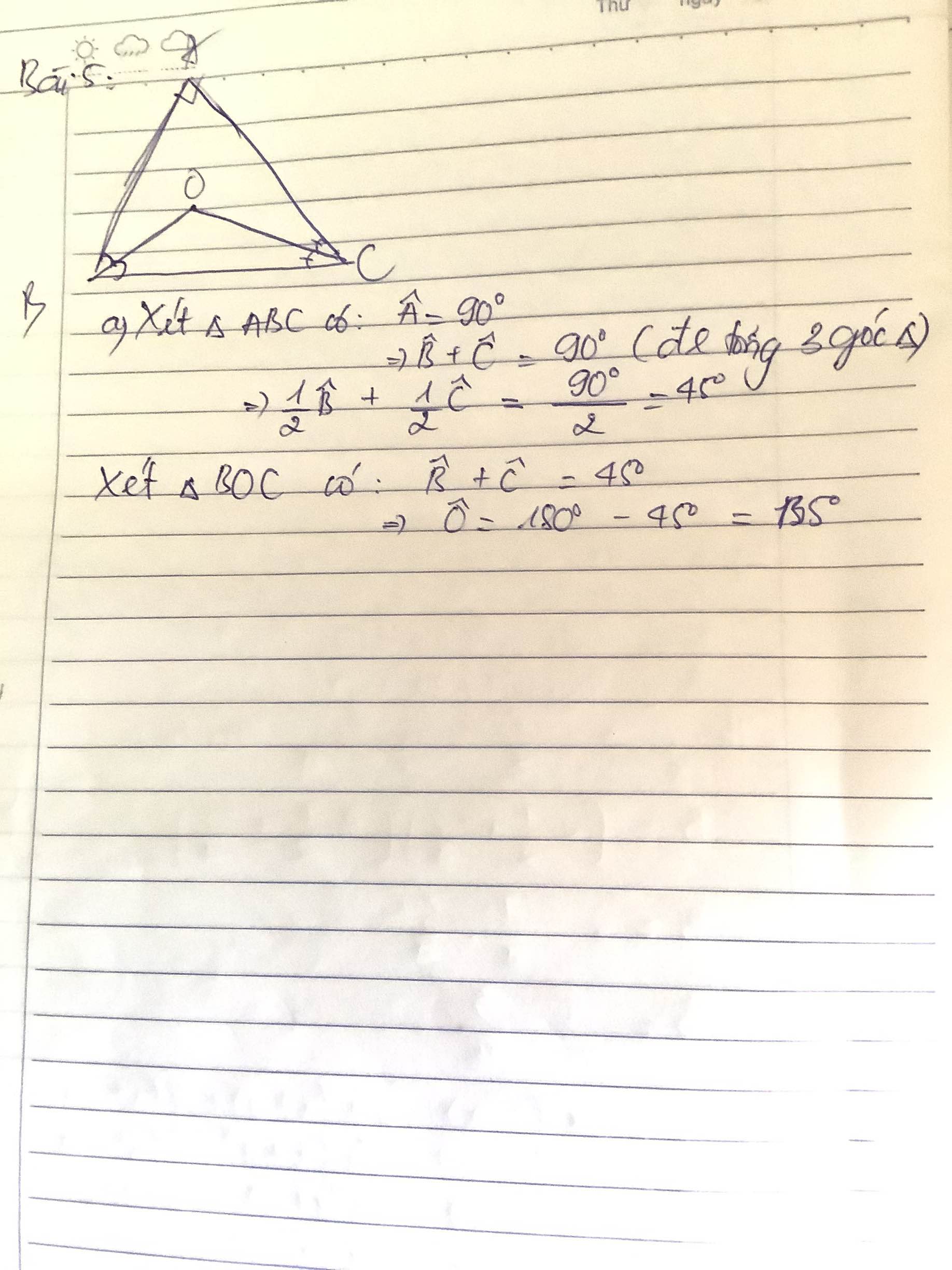
Đúng 1
Bình luận (1)
cho hình vẽ biết BH = căn 2 cm, CH= căn 8 cm . tính diện tích tam giác ABC ( vẽ giúp em hình với ạ)(em đang cần gấp lắm ạ)
Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
 vẽ hình nhanh gấp lắm đấy ạ
vẽ hình nhanh gấp lắm đấy ạ
câu 22 : a) xét ΔABN và ΔACM, ta có :
AB = AC (vì ΔABC cân tại A)
góc A là góc chung
AM = AN (gt)
⇒ ΔABN = ΔACM (c.g.c)
b) ta có : MA + MB = AB
và NA + NC = AC
mà AM = AN và AB = AC
=> MB = AB - MA (1)
=> NC = AC - NA (2)
từ (1) và (2) ⇒ MB = NC
vì ΔABN = ΔACM nên ⇒ BN = CM (2 cạnh tương ứng)
xét ΔMIB và ΔNIC, ta có :
MB = NC (cmt)
\(\widehat{MIB}=\widehat{NIC}\) (đối đỉnh)
BN = CM (cmt)
⇒ ΔMIB = ΔNIC (c.g.c)
vì ΔMIB = ΔNIC nên ⇒ IM = IN (2 cạnh tương ứng)
xét ΔAIM và ΔAIN, ta có :
AM = AN (gt)
AI là cạnh chung
IM = IN (cmt)
⇒ ΔAIM = ΔAIN (c.c.c)
⇒ \(\widehat{MAI}=\widehat{NAI}\) (2 góc tương ứng)
⇒ AI là tia phân giác của \(\widehat{A}\)
c) gọi H là giao điểm của AI và BC
xét ΔAHB và ΔAHC, ta có :
AB = AC (vì ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\) (câu b)
AH là cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)
⇒ \(\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứg) (3)
⇒ HB = HC (2 cạnh tương ứng) (4)
từ (3) và (4) ⇒ AH là đường trung trực của BC
⇒ AI là đường trung trực của BC
Đúng 0
Bình luận (0)
câu 23 : a) xét ΔABM và ΔACM, ta có :
AB = AC (vì ΔABC cân tại A)
MB = MC (vì M là trung điểm của BC)
AM là cạnh chung
⇒ ΔABM và ΔACM (c.c.c)
b) xét ΔBMD và ΔCMA, ta có :
MB = MC (vì M là trung điểm của BC)
\(\widehat{BMD}=\widehat{CMA}\) (đối đỉnh)
MD = MA (gt)
⇒ ΔBMD = ΔCMA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
đây là hình vẽ của từng câu nha :
câu 21 :
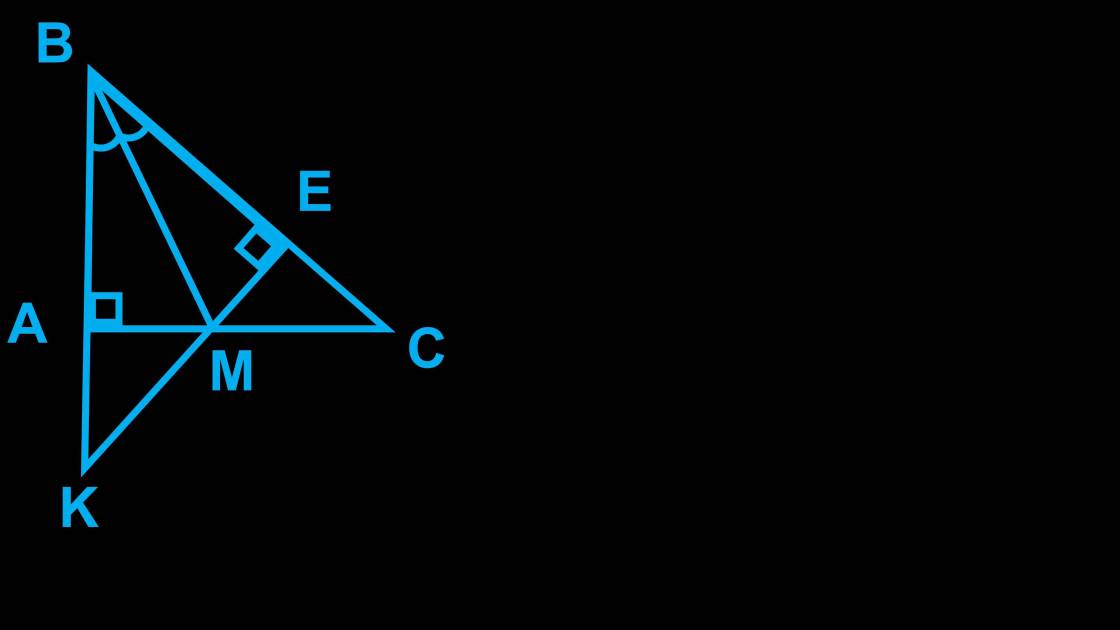
câu 22 :
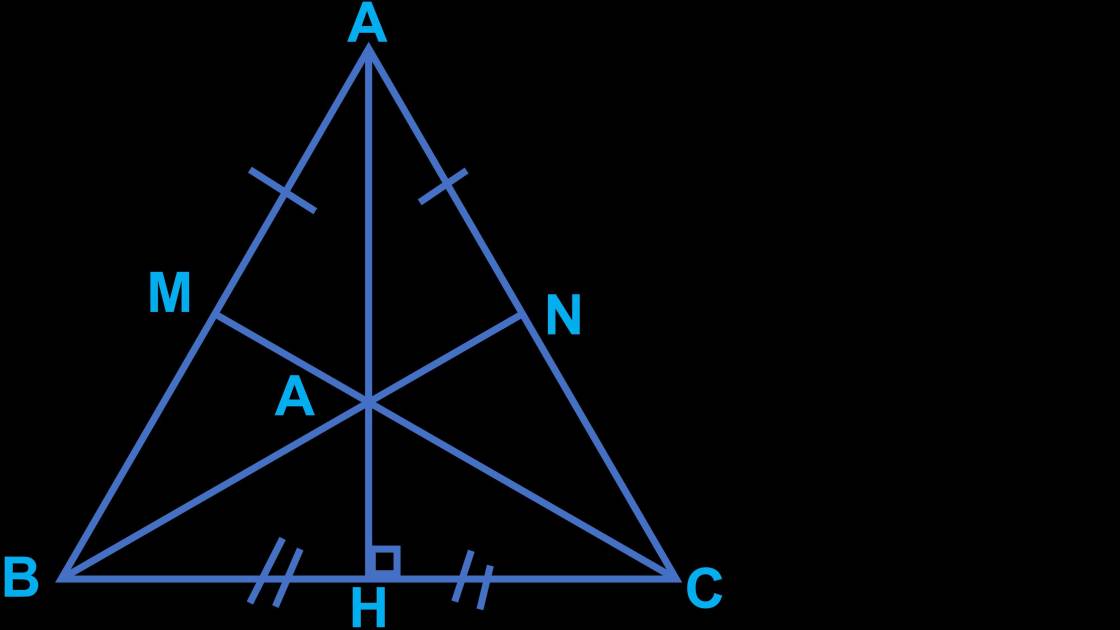
câu 23 :
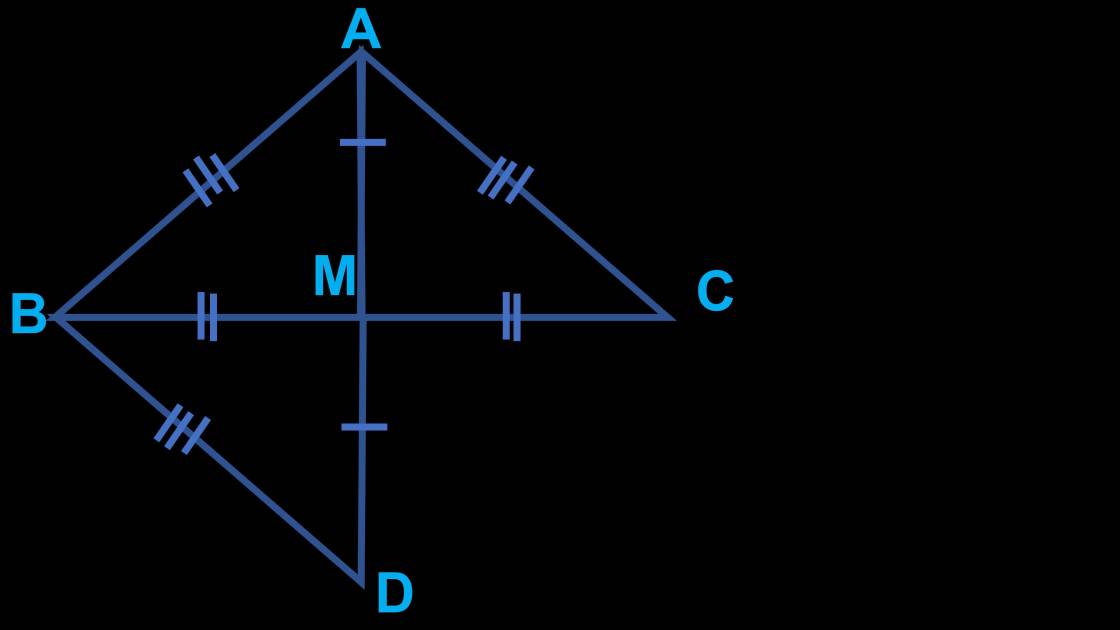
Đúng 0
Bình luận (0)
giúp em bài 1 với ạ ko cần hình vẽ ,em cần gấp lắm ạ

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
Đúng 1
Bình luận (0)
vẽ hình dùm mình với ạ. Mình cần gấp
Đọc tiếp
vẽ hình dùm mình với ạ. Mình cần gấp

Làm hết giúp mình với các bạn trình bày vẽ hình giúp mình với ạ gấp lắm ạ
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Đúng 0
Bình luận (0)