Dựng hình thang cân ABCD (AB // CD) có \(\widehat{D}=2\widehat{ACD}\), biết CD=a, đường cao AH=h
NT
Những câu hỏi liên quan
Dựng hình thang cân ABCD (AB // CD) có \(\widehat{D}=2\widehat{ACD}\), biết CD=a, đường cao AH=h
dựng hình thang cân ABCD (AB//CD) có góc D= 2 ACD, biết CD =a, đường cao AH =h
1. cho 3 điểm O, D, E. Dựng tam giác ABC sao cho O là giao điểm của 2 đường phân giác BD và CE2. Cho đường thẳng d và 2 điểm A, B nằm khác phía đối với d. Dựng điểm C thuộc d sao cho tia phân giác của widehat{ACB}nằm trên d3.Dựng hình thang cân ABCD( AB//CD) cówidehat{D} widehat{2ACD}, biết CD a, đường cao AH h
Đọc tiếp
1. cho 3 điểm O, D, E. Dựng tam giác ABC sao cho O là giao điểm của 2 đường phân giác BD và CE
2. Cho đường thẳng d và 2 điểm A, B nằm khác phía đối với d. Dựng điểm C thuộc d sao cho tia phân giác của \(\widehat{ACB}\)nằm trên d
3.Dựng hình thang cân ABCD( AB//CD) có\(\widehat{D}\)= \(\widehat{2ACD}\), biết CD = a, đường cao AH = h
Cho hình thang cân ABCD ( AB\(//\)CD) có \(\widehat{BCD}-\widehat{ACD}\)= 90o.Gọi H là chân đường cao xuất phát từ A. Ch/m AH2=HC.HD
Không cần hình vẽ nha
nhanh tick 3 tich cho
Giải:
Hình thang ABCD cân nên \(\widehat{BCD}=\widehat{ACD}\)
vì \(\widehat{ADC}-\widehat{A}=90^o\left(gt\right)\)
và \(\widehat{ADC}-\widehat{A}=90^o\)(góc ngoài)
Xét hai tam giác AHC và AHD ta thấy :
\(\widehat{H}=90^o\)
\(\widehat{ACH}=\widehat{A_1}\)(cmt)
\(\Rightarrow\Delta AHC\)gần bằng \(\Delta DHA\)
Do đó \(\frac{AH}{DH}=\frac{HC}{AH}\Rightarrow AH^2=HC.HD\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD) có \(\widehat{A}=3\widehat{D}\), \(\widehat{B}=\widehat{C}\) , AB = 3cm, CD = 4cm. Tính độ dài đường cao AH của hình thang và tính diện tích hình thang.
Vì AB // CD nên \(\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^o}{2}=90^o\)
\(\Rightarrow\)Tứ giác ABCH có 3 góc vuông là hình chữ nhật
Ta có : \(DH=DC-HC\)
\(=DC-AB\) (Vì AB = HC)
\(=4-3\)
\(=1\left(cm\right)\)
Lại có : \(\hept{\begin{cases}\widehat{A}=3\widehat{D}\\\widehat{A}+\widehat{D}=180^o\left(slt\right)\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{A}=135^o\\\widehat{D}=45^o\end{cases}}\)
\(\Rightarrow\)△AHD vuông tại H có ^ADH = 45o
\(\Rightarrow\)△AHD vuông cân tại H
\(\Rightarrow\)AH = DH
\(\Rightarrow\)AH = 1 (cm)
Vậy \(S_{ABCD}=\frac{\left(AB+CD\right)\cdot AH}{2}=\frac{\left(4+3\right)\cdot1}{2}=3,5\left(cm^2\right)\)
Xét hình thang ABCD có \(AB//CD\)(gt) có:
\(\widehat{A}+\widehat{D}=180^0\)(trong cùng phía)
Mà \(\widehat{A}=3\widehat{D}\left(gt\right)\)
\(\Rightarrow3\widehat{D}+\widehat{D}=180^0\)
\(\Leftrightarrow4\widehat{D}=180^0\)
\(\Leftrightarrow\widehat{D}=45^0\)
\(\Rightarrow\widehat{A}=3.45^0=135^0\)
Ta có:\(AB//CD\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{B}=180^0\)
\(\Leftrightarrow2\widehat{B}=180^0\)
\(\Leftrightarrow\widehat{B}=90^0\Rightarrow\widehat{C}=90^0\)
Xét tứ giác ABCH có \(\widehat{B}=\widehat{C}=\widehat{H}=90^0\left(cmt\right)\)
\(\Rightarrow\)Tứ giác ABCH là hình chữ nhật (DHNB)
\(\Rightarrow AB=CH=3cm\)(t/c) \(\Rightarrow DH=CD-CH=4-3=1\left(cm\right)\)
Xét \(\Delta AHD\)có \(\widehat{H}=90^0,\widehat{D}=45^0\left(cmt\right)\)
\(\Rightarrow\Delta AHD\)vuông cân tại A (DHNB) \(\Rightarrow AH=DH=1cm\)(t/c)
Diện tích hình thang ABCD có:
\(S_{ABCD}=\frac{\left(AB+CD\right)\times AH}{2}=\frac{\left(3+4\right)\times1}{2}=3,5\left(cm^2\right)\)
Đáp số \(3,5cm^2\)
Học tốt
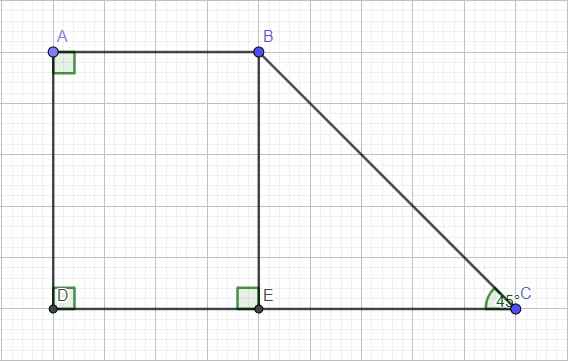
Cho hình thang \(ABCD\) có \(\widehat{A}\)=\(\widehat{D}\)=90o, \(\widehat{C}\)= 45o. Biết đường cao của hình thang bằng 4cm, \(AB+CD=10cm\). Tính 2 đáy.
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB song song với CD) có \(\widehat{A}=3.\widehat{D}\), \(\widehat{B}=\widehat{C}\), AB =3cm, CD=4cm. tính đường cao AH của hình thang và diện tích của hình thang.
Xem thêm câu trả lời
Hình thang ABCD (AB//CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân ?
Bài giải:
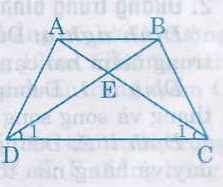
Gọi E là giao điểm của AC và BD.
∆ECD có \(\widehat{C_1}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Đúng 0
Bình luận (1)
Nối A với C, B với D. Gọi M là giao điểm của AC và BD.
Ta có: \(\widehat{MDC}=\widehat{MCD}\left(gt\right)\)
=> \(\bigtriangleup\)MDC cân tại M
=> MC = MD (1)
Ta lại có: \(\widehat{MAB}=\widehat{MCD}\) (vì hai góc so le trong và AB//CD)
\(\widehat{CDM}=\widehat{ABM}\) (vì hai góc so le trongvà AB//CD)
Mà \(\widehat{CDM}=\widehat{DCM}\left(gt\right)\) nên \(\widehat{MAB}=\widehat{MBA}\)
=> \(\bigtriangleup\) AMB cân tại M
=> MA = MB (2)
Lại có: \(AC=AM+MC\)
\(BD=BM+MD\)
Mà: \(AM=BM\left(cmt\right)\)
\(MC=MD\left(cmt\right)\)
\(\Rightarrow AC=BD\)
=> Hình thang ABCD cân.
Đúng 1
Bình luận (1)
Tứ giác ABCD có : \(\widehat{A}=\widehat{B}\), BC=AD
a) Chứng minh rằng ABCD là hình thang cân
b) Cho biết : AC ⊥ BD và đường cao AI= 4cm. Tính AB+CD
a) Xét ΔBAD và ΔABC có
AB chung
\(\widehat{BAD}=\widehat{ABC}\)(gt)
AD=BC(gt)
Do đó: ΔBAD=ΔABC(c-g-c)
Suy ra: BD=AC(hai cạnh tương ứng)
Xét ΔADC và ΔBCD có
AD=BC(gt)
AC=BD(cmt)
DC chung
Do đó: ΔADC=ΔBCD(c-c-c)
Suy ra: \(\widehat{ADC}=\widehat{BCD}\)(hai góc tương ứng)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
\(\Leftrightarrow2\cdot\widehat{BAD}+2\cdot\widehat{ADC}=360^0\)
\(\Leftrightarrow\widehat{BAD}+\widehat{ADC}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Xét tứ giác ABCD có AB//CD(cmt)
nên ABCD là hình thang(Định nghĩa hình thang)
Hình thang ABCD(AB//CD) có AC=BD(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 1
Bình luận (1)