Tính S= 1+2+22+.....+2100
S=1+52+54+....+2200
Tính tổng S=1+52 +54+.....+5200
So sánh 230+330+430và 3.2410
Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học trực tuyến OLM
a: \(25S=25+5^4+...+5^{202}\)
=>24S=5^202-1
hay \(S=\dfrac{5^{202}-1}{24}\)
b:
4^30=2^30*2^30
=(2^3)^10*(2^2)^15>8^10*3^15=(8^10*3^10)*3^5>24^10*3
=>2^30+3^30+4^30>3*24^10
Bài Toàn 16 : Tính tổng
a) S = 1 + 2 + 22 + 23 + … + 22017
b) S = 3 + 32 + 33 + ….+ 32017
c) S = 4 + 42 + 43 + … + 42017
d) S = 5 + 52 + 53 + … + 52017
a.
$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$
$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$
$\Rightarrow S=2^{2018}-1$
b.
$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$
$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$
$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
Câu c, d bạn làm tương tự a,b.
c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$
d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$
1+52+54+...+540chia hết cho 26
1+22+24+....+2100 chia hết cho 21
1+32+34+...+3100chia hết cho 82
`#3107.101107`
Gọi biểu thức trên là A
Ta có:
\(A=1+5^2+5^4+...+5^{40}\\ =1\cdot\left(1+5^2\right)+5^4\cdot\left(1+5^2\right)+...+5^{38}\cdot\left(1+5^2\right)\\ =\left(1+5^2\right)\cdot\left(1+5^4+...+5^{38}\right)\\ =26\cdot\left(1+5^4+...+5^{38}\right)\)
Vì \(26\cdot\left(1+5^4+...+5^{38}\right)\text{ }⋮\text{ }26\)
\(\Rightarrow A\text{ }⋮\text{ }26\)
_______
Gọi biểu thức trên là B
Ta có:
\(B=1+2^2+2^4+...+2^{100}\\ =1\cdot\left(1+2^2+2^4\right)+2^6\cdot\left(1+2^2+2^4\right)+...+2^{96}\cdot\left(1+2^2+2^4\right)\\ =\left(1+2^2+2^4\right)\cdot\left(1+2^6+...+2^{96}\right)\\ =21\cdot\left(1+2^6+...+2^{96}\right)\)
Vì \(21\cdot\left(1+2^6+...+2^{96}\right)\text{ }⋮\text{ }21\)
\(\Rightarrow B\text{ }⋮\text{ }21\)
_______
Gọi biểu thức trên là C
Ta có:
\(C=1+3^2+3^4+...+3^{100}\\ =1\cdot\left(1+3^2+3^4+3^6\right)+3^6\cdot\left(1+3^2+3^4+3^6\right)+...+3^{94}\cdot\left(1+3^2+3^4+3^6\right)\\ =\left(1+3^2+3^4+3^6\right)\cdot\left(1+3^6+...+3^{94}\right)\\ =820\cdot\left(1+3^6+...+3^{94}\right)\)
Vì \(820\cdot\left(1+3^6+...+3^{94}\right)\text{ }⋮\text{ }82\)
\(\Rightarrow C\text{ }⋮\text{ }82.\)
a) \(A=1+5^2+5^4+5^6...+5^{40}\)
\(\Rightarrow A=\left(1+5^2\right)+5^4\left(1+5^2\right)+...+5^{38}\left(1+5^2\right)\)
\(\Rightarrow A=26+5^4.26+...+5^{38}.26\)
\(\Rightarrow A=26\left(1+5^4+...+5^{38}\right)⋮26\)
\(\Rightarrow1+5^2+5^4+5^6...+5^{40}⋮6\left(dpcm\right)\)
b) \(B=1+2^2+2^4+2^6+...+2^{100}\)
\(\Rightarrow B=\left(1+2^2+2^4\right)+2^6\left(1+2^2+2^4\right)+...+2^{96}\left(1+2^2+2^4\right)\)
\(\Rightarrow B=21+2^6.21+...+2^{96}.21\)
\(\Rightarrow B=21\left(1+2^6+...+2^{96}\right)⋮21\)
\(\Rightarrow1+2^2+2^4+2^6+...+2^{100}⋮21\left(dpcm\right)\)
Bài C tương tự bạn tự làm nhé!
Bài toán 1: Tính giá trị các lũy thừa sau :
a) 22, 23, 24 , 25 , 26 , 27 , 28 , 29 , 210.
![]() b) 32, 33, 34 , 35.
b) 32, 33, 34 , 35.
c) 42, 43, 44.
d) 52, 53, 54.
trên đầu bài là giấu phẩy hay giấu nhân thế
\(a,2^2=4,2^3=8,2^4=16,2^5=32,2^6=64,2^7=128,2^8=256,2^9=512,2^{10}=1024\)
\(b,3^2=9,3^3=27,3^4=81,3^5=243\)
\(c,4^2=16,4^3=64,4^4=256\)
\(d,5^2=25,5^3=125,5^4=625\)
a: \(2^2=4\)
\(2^3=8\)
\(2^4=16\)
\(2^5=32\)
\(2^6=64\)
\(2^7=128\)
\(2^8=256\)
\(2^9=512\)
\(2^{10}=1024\)
b: \(3^2=9\)
\(3^3=27\)
\(3^4=81\)
\(3^5=243\)
c: \(4^2=64\)
\(4^3=256\)
\(4^4=1024\)
d: \(5^2=25\)
\(5^3=125\)
\(5^4=625\)
Cho A=1+2+22+23+24+......+2200.Hãy viết A+1 dưới dạng một lũy thừa
`A=1+2+2^2+2^3+2^4+...+2^{200}`
`=>2A=2+2^2+2^3+2^4+2^5+...+2^{201}`
`=>2A-A=(2+2^2+2^3+2^4+2^5+...+2^{201})-(1+2+2^2+2^3+2^4+...+2^{200})`
`=>A=2^{201}-1`
`=>A+1=2^{201}`
Cho mặt cầu S : x 2 + y + 5 2 + z - 2 2 = 5 và hai điểm A(2;-1;0), B(1;-3;1). Gọi E, F là giao điểm của đường thẳng AB với (S). Tính độ dài EF
![]()
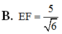
![]()
![]()
a) S=1+2+22+23+...+22022
b)S=3+32+33+...+32022
c)S=4+42+43+...+42022
d)S=5+52+53+...+52022
a) \(S=1+2+2^2+..+2^{2022}\)
\(2S=2+2^2+2^3+...+2^{2023}\)
\(2S-S=2+2^2+2^3+...+2^{2023}-1-2-2^2-...-2^{2022}\)
\(S=2^{2023}-1\)
b) \(S=3+3^2+3^3+...+3^{2022}\)
\(3S=3^2+3^3+...+3^{2023}\)
\(3S-S=3^2+3^3+....+3^{2023}-3-3^2-...-3^{2022}\)
\(2S=3^{2023}-3\)
\(\Rightarrow S=\dfrac{3^{2023}-3}{2}\)
c) \(S=4+4^2+4^3+...+4^{2022}\)
\(4S=4^2+4^3+...+4^{2023}\)
\(4S-S=4^2+4^3+...+4^{2023}-4-4^2-...-4^{2022}\)
\(3S=4^{2023}-4\)
\(S=\dfrac{4^{2023}-4}{3}\)
d) \(S=5+5^2+...+5^{2022}\)
\(5S=5^2+5^3+...+5^{2023}\)
\(5S-S=5^2+5^3+...+5^{2023}-5-5^2-...-5^{2022}\)
\(4S=5^{2023}-5\)
\(S=\dfrac{5^{2023}-5}{4}\)
tính S= 100 - 98 -96 - 94 - ... - 54 - 52
S=100-(98+96+94+...+54+52)
Số lượng số hạng là : (98-52):2+1=24
Tổng là:(98+52).24:2=1800
Do đó :S=100-1800=-1700
Làm lại nè
S=100-(98+96+94+...+54+52)
Ta có SSH là : (98-52):2+1=24
Tổng là:(98+52).24:2=1800
=>S=100-1800=-1700
a) 25 - 53 : 52 + 12 : 22
b) 5 [ ( 85 - 35 : 7 ) : 8 + 90 ] - 50
c) 2. [ ( 7 - 33 : 32 ) 22 + 99 ] - 100
d) 27 : 22 + 54 : 53 . 24 - 3 . 25
e) ( 35 . 37 ) : 310 + 5 . 24 - 73 : 7
f) 32 . [ ( 52 - 3 ) : 11 ] - 24 + 2 . 103
g) ( 62007 - 62006 ) : 62006
h) ( 52001 - 52000 ) : 52000
i) ( 72005 + 72004 ) : 72004
j) ( 57 + 75 ) . ( 68 + 86 ) . ( 24 - 42 )
k) ( 57 + 79 ) . ( 54 + 56 ) . ( 33 . 3 - 92 )
l) [ ( 52 . 23) - 72 . 2 ) : 2 ] 6 - 7 . 25
Cho S= 1/51 + 1/52+ 1/53+ 1/54 + ...........+ 1/ 98 + 1/ 99+ 1/100. So sánh S với 1/2
1/ 51 = một phần năm mốt các số khác cũng thế