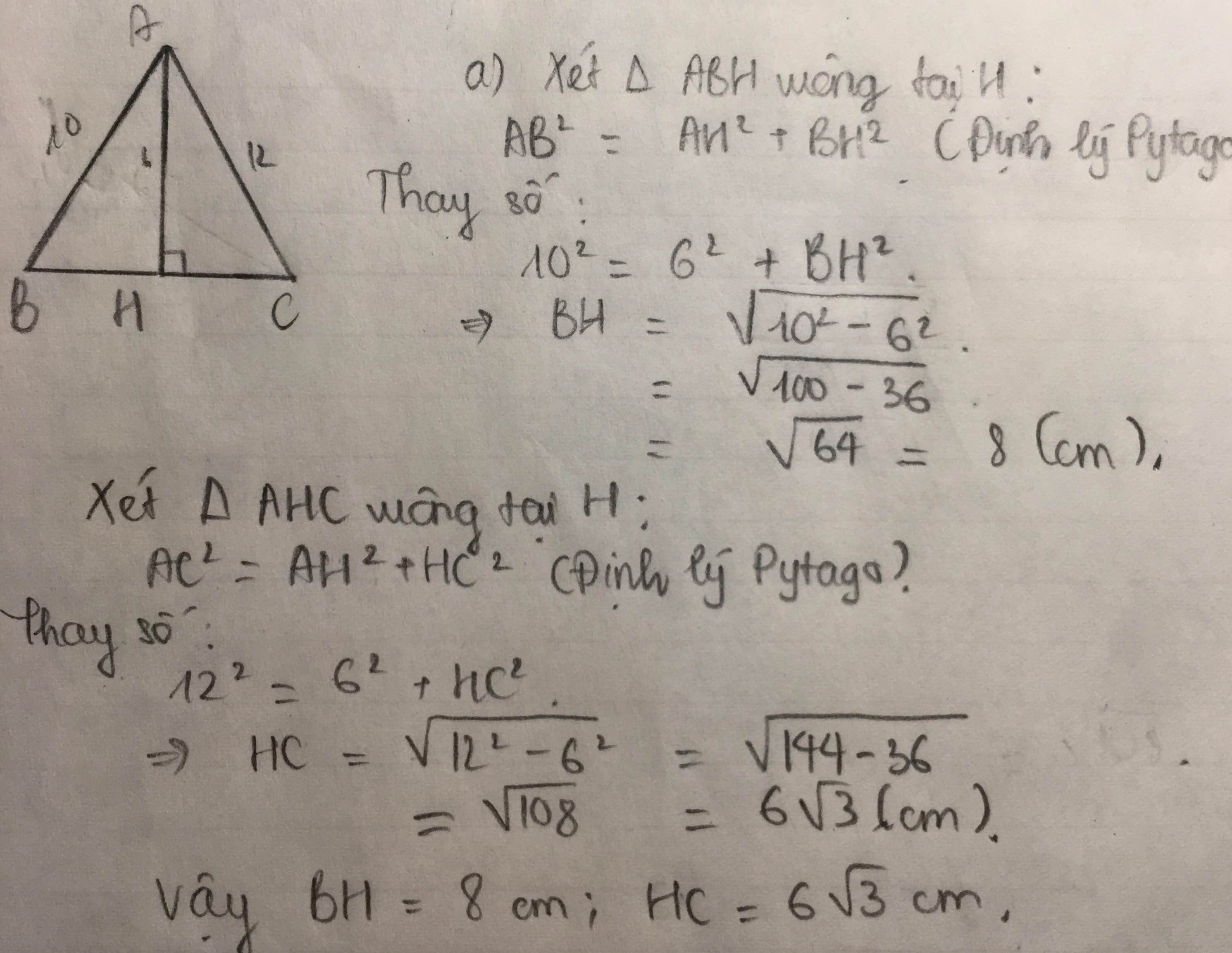Cho tam giác ABC vuông ở A có AB = 8 cm, BC = 10 cm, đường cao AH với H thuộc BC. Tính BH, CH, AH.
HD
Những câu hỏi liên quan
Cho tam giác ABC cân tại C .Kẻ AH vuông góc với BC (H thuộc BC ) Cho AH =6cm ,AB =10 cm ,AC =12 cm a)Tính BH ,CH b)Tính độ dài đường cao hạ từ C xuống AB
Cho tam giác ABC vuông tại A có AB = 6 cm ,AC = 8 cm ,AH vuông góc với BC (H thuộc BC ). Tính AH,BH,CH
Mọi người giúp mình giải bài này với
Mk cảm ơn mn nhìu
Tham khảo link này : https://olm.vn/hoi-dap/detail/246132528674.html
cho tam giác ABC cân tại C .Kẻ AH vuông góc vs BC (H thuộc BC ).Cho AH =6 cm ,AB =10 cm ,AC =12 cm
a)Tính BH và CH
b) tính độ dài đường cao hạ từ C xuống AB
Làm giúp mình câu c với!
Cho tam giác ABC vuông tại A , ( AB<AC) kẻ đường cao AH a) CM AB^2 =BH. BC.
b) CM AB.AC=AH.BC, cho AB=6, BC=10 Tính AH, CH.
c) Kẻ phân giác HD ( D thuộc AB), kẻ phân giác HE ( E thuộc AC), DE cắt AH ở I, cắt BC tại K. CM DI.EK=DK.EI
dễ quá mai mình làm cho
giờ ngủ đây
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông:
$AB^2=BH.BC$
$BH=\frac{AB^2}{BC}=\frac{9^2}{15}=5,4$ (cm)
$CH=BC-BH=15-5,4=9,6$ (cm)
$AC=\sqrt{BC^2-AB^2}=\sqrt{15^2-9^2}=12$ (cm) theo định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2$ (cm)
Đúng 3
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9.6\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot15=9\cdot12=108\)
hay AH=7,2(cm)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A có AB 9 cm , BC 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,2. Cho tam giác ABC vuông tại A có AC 5 cm , AB 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH . 3. Cho tam giác ABC vuông tại A có BC 40 cm , AC 36 cm . Tính AB , BH , CH và AH ,4. Cho tam giác ABC vuông tại A có BC 24 cm . Tính AB , AC , cho biết 2 AB -AC .5. Cho tam giác ABC vuông tại A có AH là đường cao . BH 10 cm ,...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
Đúng 1
Bình luận (0)
1. Cho tam giác ABC vuông tại A có AB 9 cm , BC 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,2. Cho tam giác ABC vuông tại A có AC 5 cm , AB 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH . 3. Cho tam giác ABC vuông tại A có BC 40 cm , AC 36 cm . Tính AB , BH , CH và AH ,4. Cho tam giác ABC vuông tại A có BC 24 cm . Tính AB , AC , cho biết 2 AB -AC .5. Cho tam giác ABC vuông tại A có AH là đường cao . BH 10 cm ,...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6 cm AC = 8 cm .Tính BC, AH, CH, BH
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Áp dụng PTG ta có: \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{6^2+8^2}=10\)
Áp dụng HTL ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{6.8}{10}=4,8\)
Áp dụng HTL ta có:\(BH.BC=AB^2\Rightarrow BC=\dfrac{6^2}{10}=3,6\)
Áp dụng HTL ta có:\(CH.BC=AC^2\Rightarrow BC=\dfrac{8^2}{10}=6,4\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại C .Kẻ AH vuông góc với BC (H thuộc BC ) Cho AH =6cm ,AB =10 cm ,AC =12 cm
a)Tính BH ,CH
b)Tính độ dài đường cao hạ từ C xuống AB
giúp mik đang cần gấp