Tìm GTNN,GTLN của y=4sin2x -3sinx -1
NC
Những câu hỏi liên quan
Tìm GTLN, GTNN của hàm số : y= -2sin2x + 3sinx -1
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=-2t^2+3t-1\)
\(\Rightarrow y_{min}=min\left\{f\left(-1\right);f\left(1\right);f\left(\dfrac{3}{4}\right)\right\}=f\left(-1\right)=-6\)
\(y_{max}=max\left\{f\left(-1\right);f\left(1\right);f\left(\dfrac{3}{4}\right)\right\}=f\left(\dfrac{3}{4}\right)=\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
Tìm GTLN, GTNN của hàm số y = -2sin2x +3sinx -1
Tìm GTLN và GTNN của hàm số
y=3sinx + 4cosx + 5
A. min y = 0, max y= 13
B. min y =0, max y=10
C. min y= 1, max y=10
D. Tất cả sai
Tìm GTLN (Max) và GTNN (Min) của biểu thức
y
3
sin
x
-
4
cos
x
(
x
∈
ℝ
)
Đọc tiếp
Tìm GTLN (Max) và GTNN (Min) của biểu thức y = 3 sin x - 4 cos x ( x ∈ ℝ )
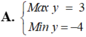
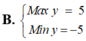
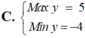
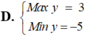
1.GTNN và GTLN của hàm số y = sinx.cosx -1 ?
2. HS y = 5 +4cosx -3sinx có GTNN và GTLN?
1.
\(y=\frac{1}{2}sin2x-1\)
Do \(-1\le sin2x\le1\Rightarrow-\frac{3}{2}\le y\le-\frac{1}{2}\)
\(y_{min}=-\frac{3}{2}\) ; \(y_{max}=-\frac{1}{2}\)
2.
\(y=5+5\left(\frac{4}{5}cosx-\frac{3}{5}sinx\right)=5+5cos\left(x+a\right)\) với \(cosa=\frac{4}{5}\)
Do \(-1\le cos\left(x+a\right)\le1\Rightarrow0\le y\le10\)
\(y_{min}=0\) ; \(y_{max}=10\)
Tìm GTLN GTNN của hs:y=3sinx-4cosx+2
Sửa: \(y=3\sin x+4\cos x+2\)
Áp dụng BĐT Bunhiacopski được:
\(\left(3\sin x+4\cos x\right)^2\le\left(3^2+4^2\right)\left(\sin x^2+\cos x^2\right)=25\)
\(\Leftrightarrow-5\le3\sin x+4\cos x\le5\\ \Leftrightarrow-3\le3\sin x+4\cos x+2\le7\\ \Leftrightarrow y_{min}=-3\\ y_{max}=7\)
Đúng 1
Bình luận (0)
Tìm GTLN và GTNN của \(M=3sinx+4cosx\)
\(M^2=\left(3sinx+4cosx\right)^2\le\left(3^2+4^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le M\le5\)
\(\Rightarrow M_{max}=5\) ; \(M_{min}=-5\)
Đúng 0
Bình luận (0)
Tìm gtnn,gtln của y=2sin^2x-3sinx+1
\(t=\sin x;t\in\left[-1;1\right]\)
Xét hàm f(t) trên [-1;1]
\(f\left(-1\right)=2+3+1=6\)
\(f\left(1\right)=2-3+1=0\)
\(f\left(\frac{3}{4}\right)=2.\frac{9}{16}-3.\frac{3}{4}+1=-\frac{1}{8}\)
\(\Rightarrow\left\{{}\begin{matrix}y_{max}=6;"="\Leftrightarrow\sin x=-1\\y_{min}=-\frac{1}{8};"="\Leftrightarrow\sin x=\frac{3}{4}\end{matrix}\right.\)
Tìm GTLN; GTNN của các hàm số
\(a,y=3-4sin^2xcos^2x\)
\(b,y=\dfrac{-2}{3sinx-5}\) trên đoạn \(\left[0;\dfrac{\pi}{2}\right]\)
a, \(y=3-4sin^2x.cos^2x=3-sin^22x\)
Đặt \(sin2x=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=3-t^2\)
\(\Rightarrow y_{min}=minf\left(t\right)=2\)
\(y_{max}=maxf\left(t\right)=3\)
Đúng 1
Bình luận (0)
b, \(y=f\left(t\right)=\dfrac{-2}{3t-5}\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y_{min}=minf\left(t\right)=\dfrac{2}{5}\)
\(y_{max}=maxf\left(t\right)=1\)
Đúng 1
Bình luận (0)




