giải dùm em vs ạ em cảm ơn nhiều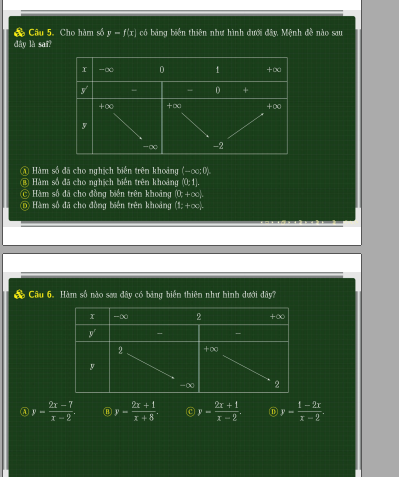


MT
Những câu hỏi liên quan
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
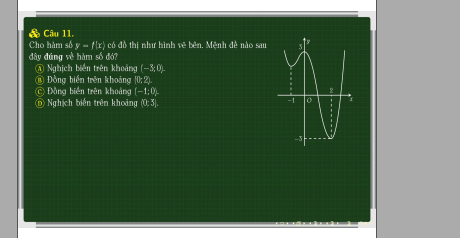
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
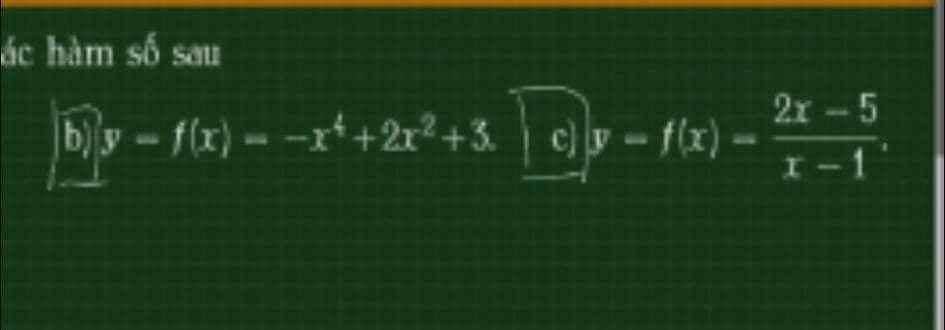

cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn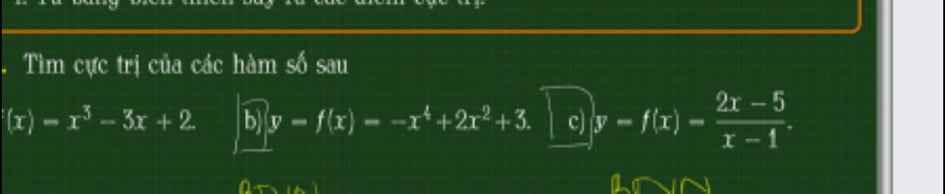
Đúng 0
Bình luận (1)
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
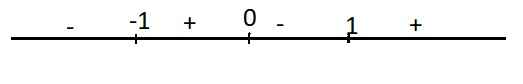
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Đúng 0
Bình luận (0)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị
Đúng 0
Bình luận (0)
giải dùm em vs ạ em cảm ơn nhiều 
giải dùm em cái này vs ạ
em cảm ơn mọi người nhiều

 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ
em cảm ơn mọi người nhiều
giải dùm em s ạ
có gì giải thích dùm em luôn em cảm ơn nhiều

14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
Đúng 1
Bình luận (0)
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)
Đúng 1
Bình luận (0)
2.
\(y'=x^2-2mx+m^2-m+1\)
\(y''=2x-2m\)
Hàm đạt cực đại tại \(x=1\) khi:
\(\left\{{}\begin{matrix}y'\left(1\right)=0\\y''\left(1\right)< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-3m+2=0\\2-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m>1\end{matrix}\right.\) \(\Rightarrow m=2\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Ai giải dùm em với ạ. Cảm ơn nhiều ạ!

giải dùm em câu 1,3,4,6 vs ạ em cảm ơn và em cần gấp lắm
1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:

Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
Đúng 0
Bình luận (0)
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
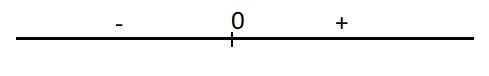
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
Đúng 0
Bình luận (0)
