Giải phương trình sau: cos10x+2cos24x+6cos3x.cosx=cosx+8cosx.cos3x
TV
Những câu hỏi liên quan
A=cos8x.cot4x-\(\frac{\left(cot^22x-1\right)}{2cot2x}\)
B=cos10x -2cos24x+6cos3x.cosx-cosx -8cosx.cos33x
Giải phương trình
\(\left(3-4\sin^2x\right)\left(3-4\sin^23x\right)=1-2\cos10x\)
Với \(sinx=0\) không phải nghiệm (vế trái bằng 9, vế phải hiển nhiên nhỏ hơn 9)
Với \(sinx\ne0\):
\(\Rightarrow\left(3sinx-4sin^3x\right)\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow sin3x\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow3sin3x-4sin^33x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin9x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin11x=sinx\)
\(\Leftrightarrow...\)
Đúng 1
Bình luận (0)
Giải phương trình lượng giác:
\(sin^22x+cos^28x=\frac{1}{2}cos10x\)
Giải phương trình sau: cos x - 3 sin x = 2
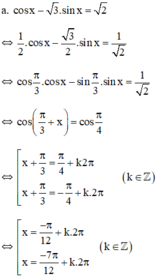
Vậy phương trình có tập nghiệm
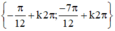 (k ∈ Z)
(k ∈ Z)
Đúng 0
Bình luận (0)
Giải phương trình sau: cosx = 2/3
cos x = 2/3 ⇒ x = ± arccos 2/3 + k2π, k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình sau: 2sinx + cosx = 1
2.sin x + cos x = 1
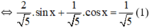
Vì 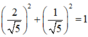 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 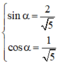
(1) trở thành:
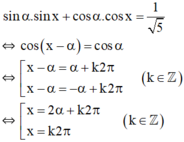
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn 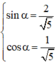
Đúng 0
Bình luận (0)
Giải phương trình sau: cosx = (-1)/2
-1/2 = cos 2π/3 nên cos x = (-1)/2
⇔ cos x = cos 2π/3
⇔ x = ±2π/3 + k2π, k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình sau:
2
cos
3
x
.
cos
x
-
4
sin
2
2
x
+
1
0
Đọc tiếp
Giải phương trình sau: 2 cos 3 x . cos x - 4 sin 2 2 x + 1 = 0
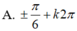
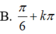
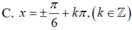
![]()
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
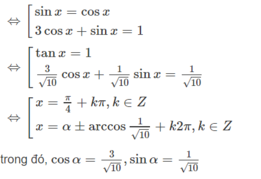
Đúng 0
Bình luận (0)


