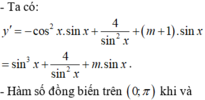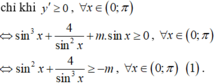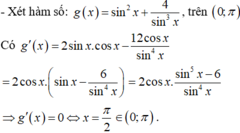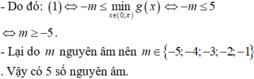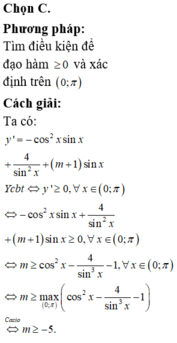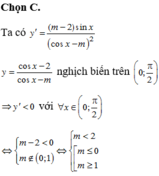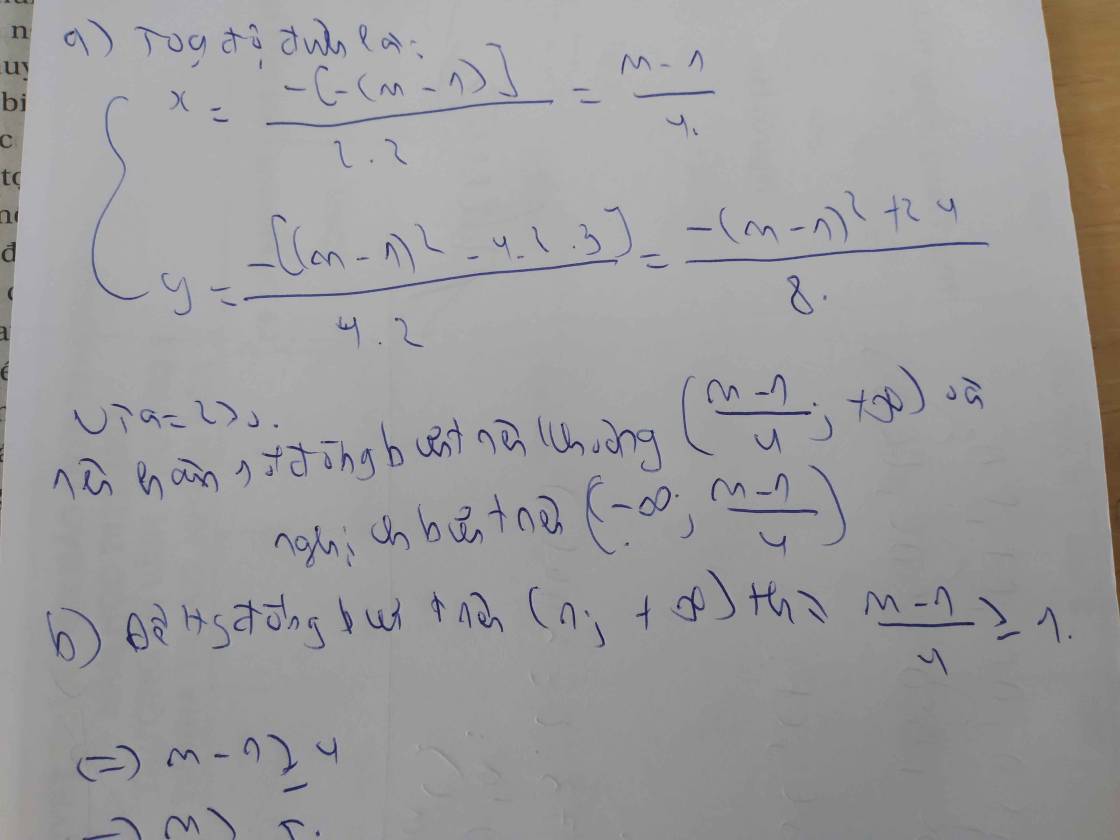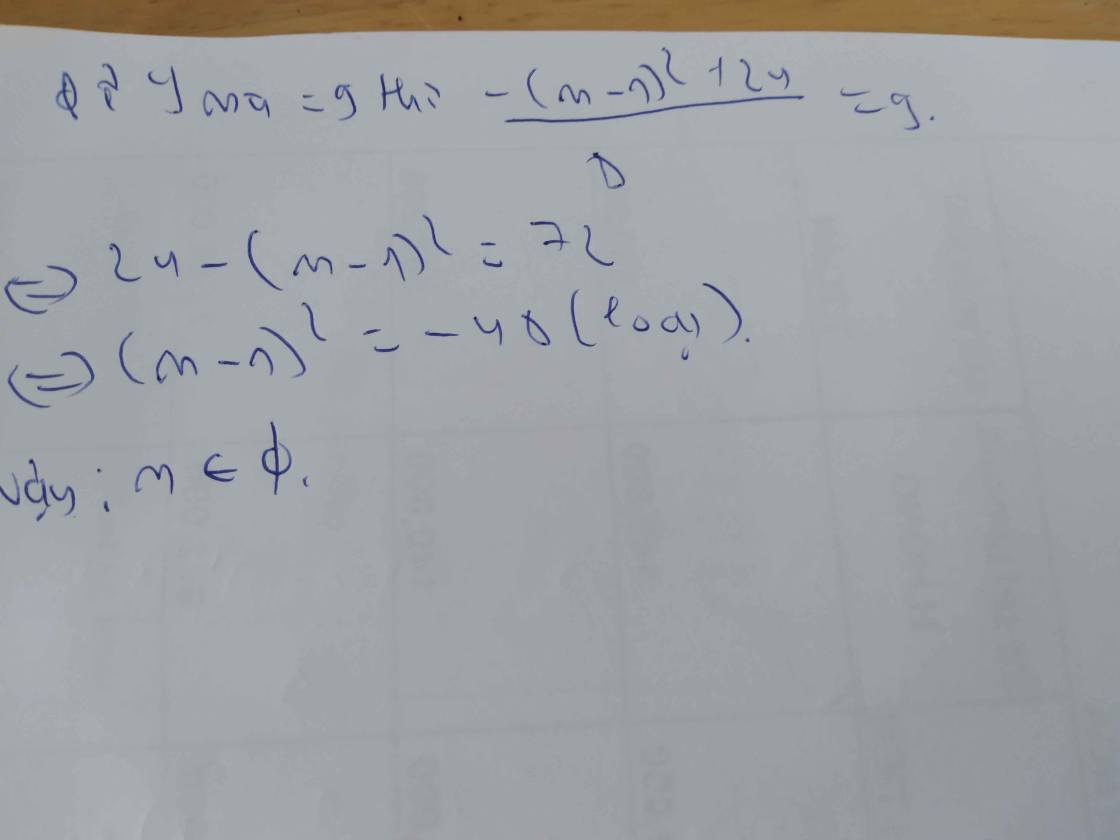Tìm m để hàm số y=(1/3)cos^3x +4cotx +(m+1)cosx đồng biến trên khoảng (0;π)
HH
Những câu hỏi liên quan
Có bao nhiêu số nguyên âm m để hàm số y = \(\dfrac{1}{3}\) cos3x - 4cotx - (m+1)cosx đồng biến trên khoảng (0; π) ?
\(y'=-3.\dfrac{1}{3}.\cos^2x.\sin x+\dfrac{4}{\sin^2x}+\left(m+1\right)\sin x=\left(\sin^2-1\right)\sin x+\dfrac{4}{\sin^2x}+m.\sin x+\sin x\)
\(=\sin^3x+\dfrac{4}{\sin^2x}+m.\sin x\)
y đồng biến trên khoảng \(\left(0;\pi\right)\) \(\Leftrightarrow y'\ge0,\forall x\in\left(0;\pi\right)\)
\(\Leftrightarrow\sin^3x+\dfrac{4}{\sin^2x}+m.\sin x\ge0\Leftrightarrow\sin^2x+\dfrac{4}{\sin^3x}\ge-m\)
\(f\left(x\right)=\sin^2x+\dfrac{4}{\sin^3x}\Rightarrow f'\left(x\right)=2.\sin x.\cos x-\dfrac{12\cos x}{\sin^4x}=2\cos x.\left(\sin x-\dfrac{6}{\sin^4x}\right)\)
\(f'\left(x\right)=0\Rightarrow2\cos x\left(\sin x-\dfrac{6}{\sin^4x}\right)=0\)
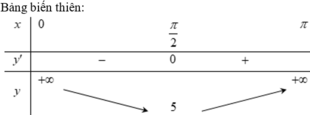
\(\Rightarrow x=\dfrac{\pi}{2}\in\left[0;\pi\right]\)
\(\Rightarrow\sin^2x+\dfrac{4}{\sin^3x}\ge-m\Leftrightarrow-m\le min_{x\in\left(0;\pi\right)}f\left(x\right)\)
\(\Leftrightarrow m\ge-5\Rightarrow m\in\left\{-5;-4;-3;-2;-1\right\}\)
Có 5 giá trị m t/m
P/s: Mới học đạo hàm nên thử sức xí :v
Đúng 2
Bình luận (0)
Có bao nhiêu số nguyên âm m để hàm số
y
1
3
c
o
s
3
x
-
4
c
o
t
x
-
(
m
+
1
)...
Đọc tiếp
Có bao nhiêu số nguyên âm m để hàm số y = 1 3 c o s 3 x - 4 c o t x - ( m + 1 ) cos x đồng biến trên khoảng ( 0 ; π ) ?
A. 5
B. 2
C. vô số
D. 3
Có bao nhiêu số nguyên dương m để hàm số
y
1
3
cos
3
x
-
4
cot
x
-
(
m
+
1
)
cos
x
đồng biến trên khoảng
0
;
π
? A. 7 B. 4 C. vô số D. 8
Đọc tiếp
Có bao nhiêu số nguyên dương m để hàm số y = 1 3 cos 3 x - 4 cot x - ( m + 1 ) cos x đồng biến trên khoảng 0 ; π ?
A. 7
B. 4
C. vô số
D. 8
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
-
2
cos
x
-
m
đồng biến trên khoảng (0;
π
2
). A.. B.. C. hoặc . D..
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x - 2 cos x - m đồng biến trên khoảng (0; π 2 ).
A.![]() .
.
B.![]() .
.
C.![]() hoặc
hoặc ![]() .
.
D.![]() .
.
Chọn D
Đặt ![]() ,
, ![]() thì
thì ![]() . Ta có:
. Ta có:
![]()
![]()
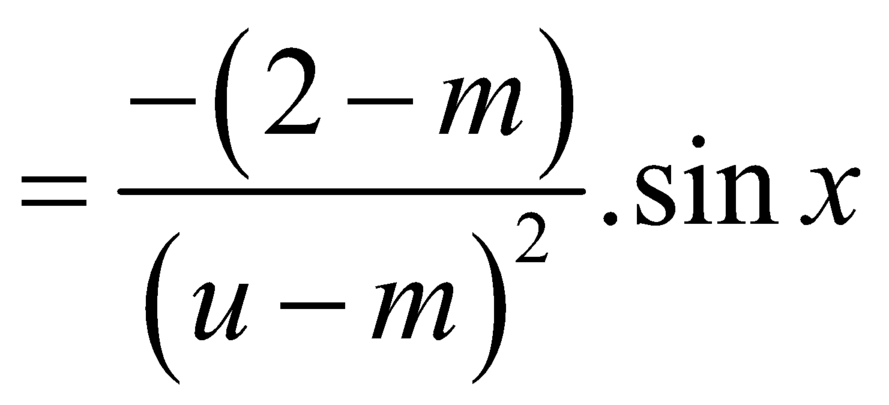 .
.
Vì ![]() nên ycbt
nên ycbt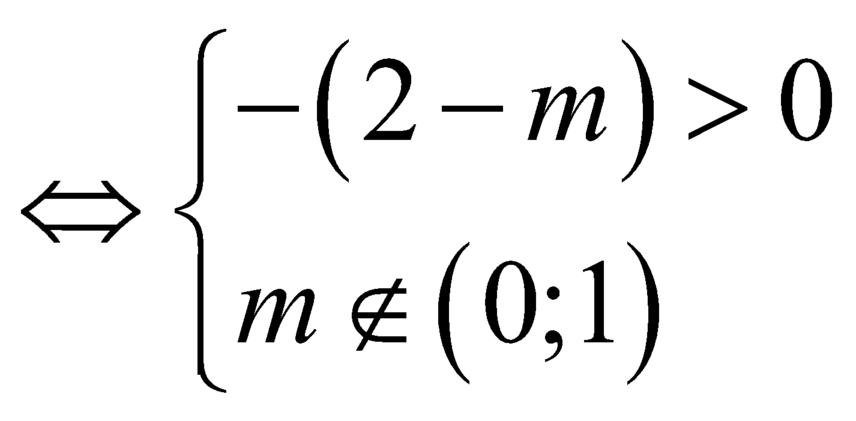 .
.
Đến đây giải được: ![]() .
.
Đúng 0
Bình luận (0)
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
m
cos
x
+
1
cos
x
+
m
đồng biến trên khoảng (0;
π
3
). A. (-1; 1) B.
-
∞
;
...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng (0; π 3 ).
A. (-1; 1)
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 2 ; 1)
D. (-1; - 1 2 )
Tìm m để hàm số
y
cos
x
-
2
cos
x
-
m
nghịch biến trên khoảng
0
;
π
2
A.
m
≥
2...
Đọc tiếp
Tìm m để hàm số y = cos x - 2 cos x - m nghịch biến trên khoảng 0 ; π 2
A. m ≥ 2 m ≤ - 2
B. m > 2
C. m ≤ 0 1 ≤ m < 2
D. - 1 < m < 1
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
m
cos
x
+
1
cos
x
+
m
đồng biến trên khoảng
0
;
π
3
A. ...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng 0 ; π 3
A. - 1 ; 1
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 ; - 1 2 )
D. - 1 ; - 1 2
Đạo hàm y 0 −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 0, ∀x ∈ (0; 3) ⇔ m 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) 6x − 6; f 0 (x) 0 ⇔ x 1. Khi đó f(0) 1, f(3) 10, f(1) −2, suy ra max [0;3] f(x) f(3) 10. Do đó (∗) ⇔ m max [0;3] f(x) ⇔ m 10. Vậy với m 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Đọc tiếp
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).