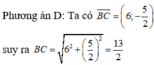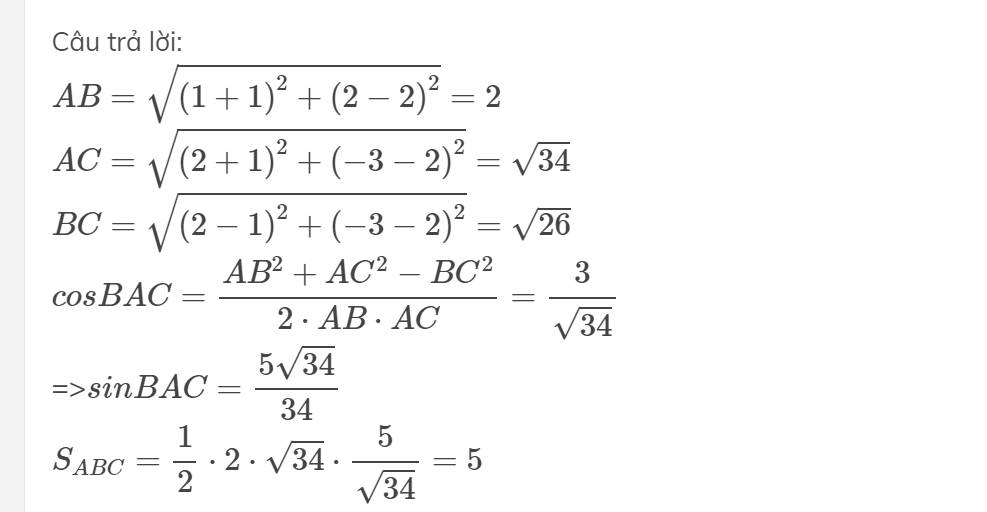Chọn C

C

C

Lời giải:
\(\overrightarrow{a}=-2\overrightarrow{i}+3\overrightarrow{j}=-2(1,0)+3(0,1)=(-2.1+3.0, -2.0+3.1)=(-2,3)\)

Do I thuộc Oy nên tọa độ có dạng \(I\left(0;y\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(1;3-y\right)\\\overrightarrow{BI}=\left(2;y+3\right)\end{matrix}\right.\)

\(\Rightarrow IA+IB=\sqrt{1+\left(3-y\right)^2}+\sqrt{2^2+\left(y+3\right)^2}\ge\sqrt{\left(1+2\right)^2+\left(3-y+y+3\right)^2}=3\sqrt{5}\)

Dấu "=" xảy ra khi \(\dfrac{2}{1}=\dfrac{y+3}{3-y}\Rightarrow y=1\Rightarrow I\left(0;1\right)\)

Cách khác:

Do A và B nằm khác phía so với Oy

\(\Rightarrow IA+IB\) đạt giá trị nhỏ nhất khi A, I, B thẳng hàng

Hay I là giao điểm của đường thẳng AB và trục Oy

\(\overrightarrow{BA}=\left(3;6\right)=3\left(1;2\right)\Rightarrow\) đường thẳng AB nhận \(\left(2;-1\right)\) là 1 vtpt

Phương trình AB:

\(2\left(x-1\right)-1\left(y-3\right)=0\Leftrightarrow2x-y+1=0\)

I là giao điểm AB và Oy nên tọa độ là nghiệm của hệ:

\(\left\{{}\begin{matrix}2x-y+1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)

\(\Rightarrow I\left(0;1\right)\)

Tham khảo

Chọn D.

\(AB=\sqrt{\left(1+1\right)^2+\left(2-2\right)^2}=2\)

\(AC=\sqrt{\left(2+1\right)^2+\left(-3-2\right)^2}=\sqrt{34}\)

\(BC=\sqrt{\left(2-1\right)^2+\left(-3-2\right)^2}=\sqrt{26}\)

\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{3}{\sqrt{34}}\)

=>\(sinBAC=\dfrac{5\sqrt{34}}{34}\)

\(S_{ABC}=\dfrac{1}{2}\cdot2\cdot\sqrt{34}\cdot\dfrac{5}{\sqrt{34}}=5\)