cho hàm số y=x3-5x2+2 (C) .Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua điểm A(0;2)
NT
Những câu hỏi liên quan
Gọi (C) là đồ thị của hàm số
y
x
3
−
5
x
2
+
2
. Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó song song với đường thẳng y - 3x + 1 A. y -3x – 7 B.
y
−
3
x
+
67
27
C. Cả A và B đúng D. Đáp án khác
Đọc tiếp
Gọi (C) là đồ thị của hàm số y = x 3 − 5 x 2 + 2 . Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó song song với đường thẳng y = - 3x + 1
A. y = -3x – 7
B. y = − 3 x + 67 27
C. Cả A và B đúng
D. Đáp án khác
Vì phương trình tiếp tuyến song song với đường thẳngy =-3x + 1nên nó có hệ số góc là -3
Do đó f ' x = 3 x 2 − 10 x = − 3 ⇔ 3 x 2 − 10 x + 3 = 0
⇔ x = 1 3 x = 3
Với x = 1 3 thì y 0 = 40 27 Vậy phương trình tiếp tuyến là: y = − 3 x − 1 3 + 40 27 = − 3 x + 67 27
Với x=3thì y 0 = - 16 Vậy phương trình tiếp tuyến là: y = -3(x- 3) – 16 = - 3x – 7
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho hàm số y=\(2x^4-4x^2-1\) có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết
a) tiếp tuyến vuông góc với đường thẳng \(x-48y+1=0\)
b) tiếp tuyến đi qua \(A\left(1;-3\right)\)
c) tiếp tuyến tiếp xúc voi (C) tại 2 điểm phân biệt
\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
Đúng 1
Bình luận (0)
Cho hàm số \(y=\left(2-x\right)^2x^2\) có đồ thị (C)
a. Viết phương trình tiếp tuyến tại giao điểm (C) với Parabol \(y=x^2\)
b. Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(2;0)
Ta có \(y=x^4-4x^3+4x^2\Rightarrow4x^3-12x^2+8x\)
a. PTHD giao điểm của (C) và Parabol \(y=x^2\) :
\(x^4-4x^3+4x^2=x^2\Leftrightarrow x^2\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x=0;x=1;x=3\)
* \(x=0\) ta có phương trình tiếp tuyến là \(y=0\)
* \(x=2\) ta có phương trình tiếp tuyến là \(y=1\)
* \(x=3\) ta có phương trình tiếp tuyến là \(y=24x-63\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k \(\Rightarrow d:y=k\left(x-2\right)\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\left(2-x\right)^2x^2-k\left(x-2\right)\\4x\left(x-2\right)\left(x-1\right)=k\end{cases}\) có nghiệm
Thay k vào phương trình thứ nhất ta có :
\(x^4-4x^3+4x^2=\left(x-2\right)\left(4x^3-12x^2+8x\right)\)
\(\Leftrightarrow x\left(3x-4\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow x=0;x=2;x=\frac{4}{3}\)
* \(x=0\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)
* \(x=2\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)
* \(x=\frac{4}{3}\Rightarrow k=-\frac{32}{27}\Rightarrow\) Phương trình tiếp tuyến \(y=-\frac{32}{27}x+\frac{64}{27}\)
Đúng 0
Bình luận (0)
Cho hàm số
y
−
x
3
+
2
x
2
+
2
có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng
y
x
+
2.
A.
y
x
+
68
27
.
B.
y
x
+
2....
Đọc tiếp
Cho hàm số y = − x 3 + 2 x 2 + 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng y = x + 2.
A. y = x + 68 27 .
B. y = x + 2.
C. y = x + 50 27 .
D. y = x − 1 3 .
Đáp án C.
Ta có:
y ' = − 3 x 2 + 4 x ; y ' = 1 ⇔ − 3 x 2 + 4 x = 1 ⇔ x = 1 x = 1 3 .
Khi x = 1, tiếp tuyến có phương trình y = x + 2 trùng với đường thẳng y = x + 2.
Khi x = , tiếp tuyến có phương trình y = x + 50 27 .
Đúng 0
Bình luận (0)
Cho
∆
:
y
-
3
x
-
8
. Viết phương trình tiếp tuyến (d) của
(
C
)
:
y
x
3
-
5
x
2
+
1
biết
(
d
)
∥
∆
Đọc tiếp
Cho ∆ : y = - 3 x - 8 . Viết phương trình tiếp tuyến (d) của ( C ) : y = x 3 - 5 x 2 + 1 biết ( d ) ∥ ∆
![]()
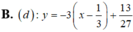
![]()
![]()
cho đường tròn (c): x + y^ _2x+6y+5=0 viết phương trình tiếp tuyến của (c) biết tiếp tuyến đi qua điểm m(–2;–4)
Em ghi lại pt đường tròn nhé, bị lỗi rồi
Đúng 0
Bình luận (0)
Cho hàm số: y = x3 - 3x2 + 1. Tìm k để có 2 tiếp tuyến của đồ thị có cùng hệ số góc k. Viết phương trình đường thẳng đi qua 2 tiếp điểm theo k
" Tìm k để có 2 tiếp tuyến của đồ thị có cùng hệ số góc k"
Đọc câu này mà não load không nổi luôn :D
Đọc đi đọc lại không hiểu đề bài muốn nói đến điều gì
Đúng 2
Bình luận (4)
Cho hàm số y = x 3 + 3 x 2 + 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C): Biết rằng tiếp tuyến có hệ số góc là 9.
Cho hàm số y = x 3 + 3 x 2 + 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C): Tiếp tuyến vuông góc với đường thẳng (d’ ) : x + 9y + 2013 = 0
Gọi x 0 , y 0 là tọa độ tiếp điểm của đồ thị hàm số (C ).
- Đường thẳng (d'): x + 9y + 2013 = 0
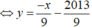
có hệ số góc
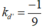
- Vì tiếp tuyến vuông góc với đường thẳng d’ nên:
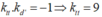
→ Bài toán trở thành viết phương trình tiếp tuyến biết hệ số góc của tiếp tuyến là 9.
- Theo 4) có hai tiếp tuyến có hệ số góc k = 9 là:
y = 9x – 4 và y = 9x + 28.
Đúng 0
Bình luận (0)
Cho hàm số y = x 3 + 3 x 2 + 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C): Tiếp tuyến song song với đường thẳng (d ): 27x - 3y + 5 = 0
Gọi x 0 , y 0 là tọa độ tiếp điểm của đồ thị (C ) và tiếp tuyến ∆.
- Đường thẳng d :
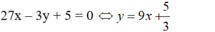
- Vì tiếp tuyến ∆ // d nên tiếp tuyến ∆ có hệ số góc k= 9.
- Theo 4) có hai tiếp tuyến có hệ số góc k = 9 là:
y = 9x – 4 và y = 9x + 28.
Đúng 0
Bình luận (0)





