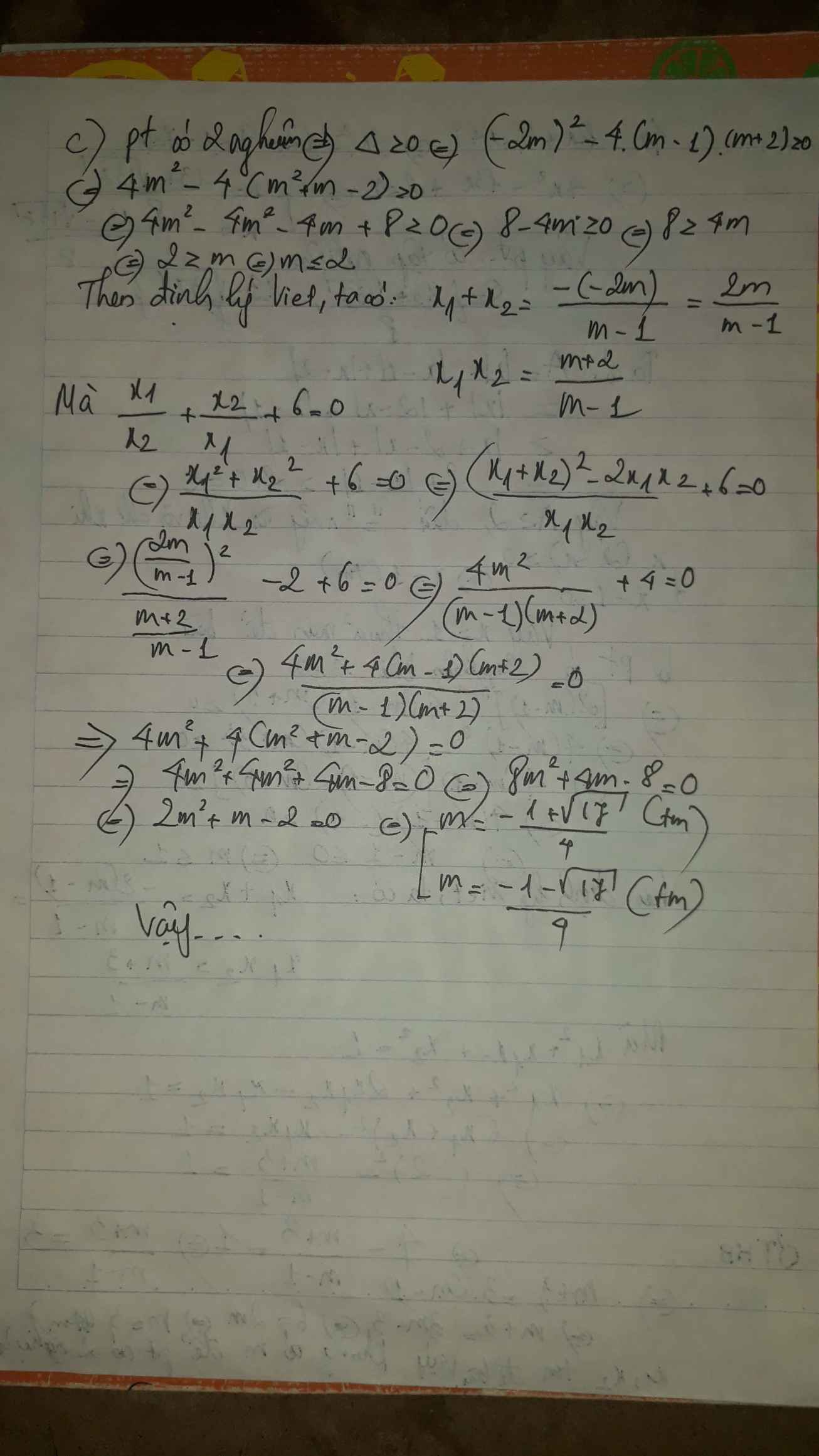\(\left|X-2\right|\left(X-1\right)+m=0\).Tìm m để phương trình có 3 nghiệm phân biệt
H24
Những câu hỏi liên quan
Tìm m để phương trình: \(\left|x-1\right|\left(x-3\right)-m=0\) có 3 nghiệm phân biệt
cho phương trình \(\left(m+1\right)x^2-2\left(m+1\right)x+m-3=0\)
a, giải phương trình khi m = 3
b, tìm m để phương trình có 2 nghiệm phân biệt \(x_1;x_2\)thoả mãn \(\left(4x_1+1\right)\left(4x_2+1\right)=18\)
a, Thay m vào pt ta được :
(3+1).x2-2(3+1).x+3-3=0
\(\Leftrightarrow\)4x2-8x=0
\(\Leftrightarrow4x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy m=3 phương trình có 2 nghiệm là 0 và 2
b, Theo Vi et ta có :
\(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m-3}{m+1}\\x_1+x_2=\dfrac{2\left(m+1\right)}{m+1}\end{matrix}\right.\left(vớim\ne-1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1.x_2=\dfrac{m-3}{m+1}\\x_1+x_2=2\end{matrix}\right.\) (1)
Ta có : (4x1+1)(4x2+1)=18
\(\Leftrightarrow16x_1.x_2+4x_1+4x_2+1=18\)
\(\Leftrightarrow16.x_1.x_2+4\left(x_1+x_2\right)=17\) (2)
Thay (1) vào (2) ta được :
16.\(\dfrac{m-3}{m+1}+4.2=17\)
\(\Leftrightarrow\dfrac{16m-48}{m+1}=9\)
\(\Leftrightarrow9\left(m+1\right)=16m-48\)
\(\Leftrightarrow9m+9=16m-48\)
\(\Leftrightarrow7m=57\)
\(\Leftrightarrow m=\dfrac{57}{7}\) (thỏa mãn m\(\ne-1\))
Vậy ..
Đúng 2
Bình luận (0)
Tìm tham số m để phương trình sau có đúng 2 nghiệm phân biệt: \(x^3-\left(1+m\right)x^2+\left(m-1\right)x+2m-2=0\)
b Tìm m để phương trình left(m-1right)x^2+2left(m-1right)x+m+30 có hai nghiệm x1,x2 thỏa mãn x_1^2+x_1.x_2+x_2^21c Tìm m để phương trình left(m-1right)x^2-2mx+m+20 có hai nghiệm x1,x2 phân biệt thỏa mãn dfrac{x_1}{x_2}+dfrac{x_2}{x_1}+60d Tìm m để phương trình 3x^2+4left(m-1right)x+m^2-4m+10 có hai nghiệm phân biệt x1,x2 thỏa mãn dfrac{1}{x_1}+dfrac{1}{x_2}dfrac{1}{2} (x1+x2)
Đọc tiếp
b Tìm m để phương trình \(\left(m-1\right)x^2+2\left(m-1\right)x+m+3=0\) có hai nghiệm x1,x2 thỏa mãn \(x_1^2+x_1.x_2+x_2^2=1\)
c Tìm m để phương trình \(\left(m-1\right)x^2-2mx+m+2=0\) có hai nghiệm x1,x2 phân biệt thỏa mãn \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}+6=0\)
d Tìm m để phương trình \(3x^2+4\left(m-1\right)x+m^2-4m+1=0\) có hai nghiệm phân biệt x1,x2 thỏa mãn \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\) (x1+x2)
b) phương trình có 2 nghiệm \(\Leftrightarrow\Delta'\ge0\)
\(\Leftrightarrow\left(m-1\right)^2-\left(m-1\right)\left(m+3\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-m^2-3m+m+3\ge0\)
\(\Leftrightarrow-4m+4\ge0\)
\(\Leftrightarrow m\le1\)
Ta có: \(x_1^2+x_1x_2+x_2^2=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)\\x_1x_2=\dfrac{c}{a}=m+3\end{matrix}\right.\)
\(\Leftrightarrow\left[-2\left(m-1\right)^2\right]-2\left(m+3\right)=1\)
\(\Leftrightarrow4m^2-8m+4-2m-6-1=0\)
\(\Leftrightarrow4m^2-10m-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{5+\sqrt{37}}{4}\left(ktm\right)\\m_2=\dfrac{5-\sqrt{37}}{4}\left(tm\right)\end{matrix}\right.\Rightarrow m=\dfrac{5-\sqrt{37}}{4}\)
Đúng 1
Bình luận (1)
Tìm m để phương trình \(\left(x^2-4x\right)^2-3\left(x-2\right)^2+m=0\) có 4 nghiệm phân biệt
\(\Leftrightarrow\left[\left(x-2\right)^2-4\right]^2-3\left(x-2\right)^2+m=0\)
\(\left(x-2\right)^2=t\ge0\Rightarrow pt\Leftrightarrow\left(t-4\right)^2-3t+m=0\)
\(\Leftrightarrow t^2-11t+16+m=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=11^2-4\left(16+m\right)>0\\x_1+x_2=11>0\left(tm\right)\\x_1x_2=16+m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{57}{4}\\m< 16\end{matrix}\right.\Leftrightarrow m< \dfrac{57}{4}\)
Đúng 0
Bình luận (0)
cho phương trình:\(x^3-\frac{1}{x^3}-\left(m-1\right)\left(x-\frac{1}{x}\right)+m-3=0\)Tìm m để phương trình có đúng 2 nghiệm dương phân biệt
cho phương trình \(x^2-6\left(m-1\right)x+9\left(m-3\right)=0\left(1\right)\)
a, giải phương trình (1) khi m=2
b, tìm các giá trị của m để phương trình (1) có 2 nghiệm phân biệt thoả mãn \(x_1+x_2=2x_1.x_2\)
a. Khi m=2 thì (1) có dạng :
\(x^2-6\left(2-1\right)x+9\left(2-3\right)=0\\ \Leftrightarrow x^2-6x-9=0\\ \Leftrightarrow\left(x-3\right)^2=18\Leftrightarrow x-3=\pm\sqrt{18}\\ \Leftrightarrow x=3\pm3\sqrt{2}\)
Vậy với m=2 thì tập nghiệm của phương trình là \(S=\left\{3\pm3\sqrt{2}\right\}\)
b. Coi (1) là phương trình bậc 2 ẩn x , ta có:
\(\text{Δ}'=\left(-3m+3\right)^2-1\cdot9\left(m-3\right)=9m^2-18m+9-9m+27\\ =9m^2-27m+36=\left(3m-\dfrac{9}{2}\right)^2+\dfrac{63}{4}>0\)
Nên phương trình (1) luôn có 2 nghiệm x1,x2 thỏa mãn:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(m-1\right)\\x_1x_2=9\left(m-3\right)\end{matrix}\right.\left(2\right)\)
Vì
\(x_1+x_2=2x_1x_2\\ \Leftrightarrow6\left(m-1\right)=18\left(m-3\right)\Leftrightarrow m-1=3m-9\\ \Leftrightarrow2m=8\Leftrightarrow m=4\)
Vậy m=4
Đúng 2
Bình luận (0)
b) Ta có: \(\text{Δ}=\left[-6\left(m-1\right)\right]^2-4\cdot1\cdot9\left(m-3\right)\)
\(=\left(6m-6\right)^2-36\left(m-3\right)\)
\(=36m^2-72m+36-36m+108\)
\(=36m^2-108m+144\)
\(=\left(6m\right)^2-2\cdot6m\cdot9+81+63\)
\(=\left(6m-9\right)^2+63>0\forall m\)
Suy ra: Phương trình luôn có hai nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(m-1\right)=6m-6\\x_1\cdot x_2=9\left(m-3\right)=9m-27\end{matrix}\right.\)
Ta có: \(x_1+x_2=2x_1\cdot x_2\)
\(\Leftrightarrow6m-6=2\left(9m-27\right)\)
\(\Leftrightarrow6m-6-18m+54=0\)
\(\Leftrightarrow-12m+48=0\)
\(\Leftrightarrow-12m=-48\)
hay m=4
Vậy: m=4
Đúng 0
Bình luận (0)
Cho phương trình: \(x^2+2\left(m+1\right)x-8=0\left(1\right)\). Tìm \(m\) để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2=x_2\)
cái này tínhd đen ta r áp dụng hệ thức vi ét
Đúng 0
Bình luận (0)
cái biêủ thức đề bài biến đổi để kết hợp với pt tổng trong Viet ra hệ pt tìm ra x1 x2 ròi that vào pt tích trong viet
Đúng 0
Bình luận (0)
Tìm m để phương trình \(-x^2+2\left(m-1\right)x+m-3=0\) có hai nghiệm phân biệt
Phương trình có 2 nghiệm pb khi:
\(\Delta'=\left(m-1\right)^2+m-3>0\)
\(\Leftrightarrow m^2-m-2>0\)
\(\Rightarrow\left[{}\begin{matrix}m< -1\\m>2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm m để phương trình \(7x^3+\left(2m-9\right)x^2-\left(m^2+2m-2\right)x-2=0\) có 3 nghiệm phân biệt