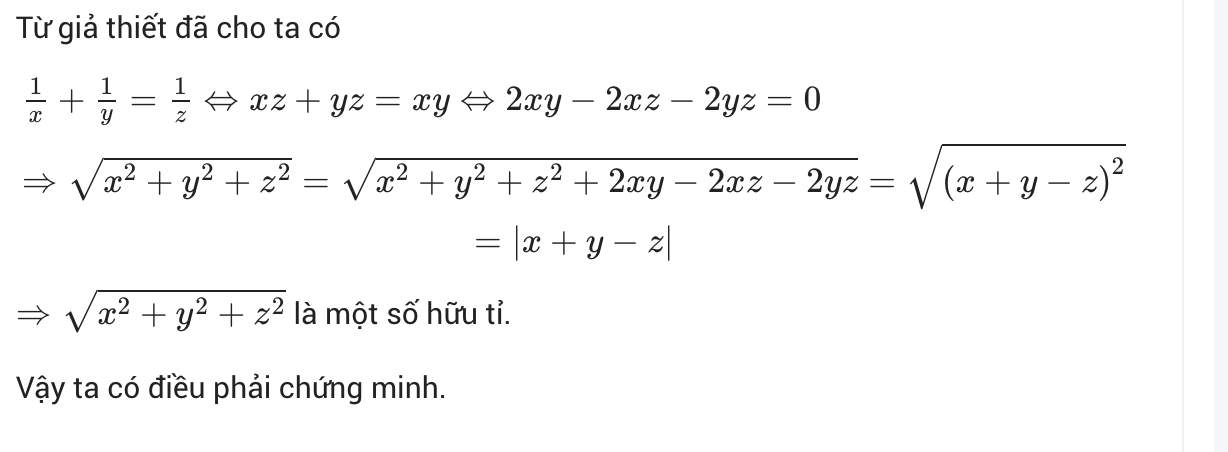chứng minh rằng không tồn tại các sô hữu tỉ x,y,z tỏa mãn x^2 + y^2 +z^2 + x + 3y +5z +7 =0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
DA
Những câu hỏi liên quan
Chứng minh rằng không tồn tại các số hữu tỉ nào thỏa mãn: \(x^2+y^2+z^2+x+3y+5z=0\)
T nghĩ đề nên là số 9 sẽ hợp lí hơn
\(x^2+y^2+z^2+x+3y+5z+9=0\)
\(\Rightarrow\left(x^2+x+\dfrac{1}{4}\right)+\left(y^2+3y+\dfrac{9}{4}\right)+\left(z^2+5z+\dfrac{25}{4}\right)+\dfrac{1}{4}=0\)
\(\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\left(y+\dfrac{3}{2}\right)^2+\left(z+\dfrac{5}{2}\right)^2=-\dfrac{1}{4}\Leftrightarrow pt\) vô nghiệm
Đúng 0
Bình luận (0)
Cho các số nguyên x,y,z khác không, thỏa mãn x+y+z=0.
Chứng minh rằng căn (1/ x^2 + 1/y^2 + 1/z^2) là số hữu tỉ
Ta có:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)
\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ
Đúng 0
Bình luận (0)
Cho các sô hữu tỉ x, y, z thỏa mãn điều kiện: x+y+z=0
CMR: A=1/x^2+1/y^2+1/z^2 là bình phương của 1 số hữu tỉ
A=\(\frac{x^2y^2+x^2z^2+y^2z^2}{x^2y^2z^2}\)
Ta có:\(x^2y^2+x^2z^2+y^2z^2=\left(xy+yz+zx\right)^2-2\left(xyz\right)\left(x+y+z\right)\)
\(=\left(xy+yz+zx\right)^2\)(do x+y+z=0)
Do đó A=\(\frac{\left(xy+yz+zx\right)^2}{\left(xyz\right)^2}=\left[\frac{\left(xy+yz+zx\right)}{xyz}\right]^2\)
Nên A là số chính phương(ĐCCM)
Đúng 0
Bình luận (0)
chứng minh rằng không tồn tại các số tự nhiên x;y;z thỏa mãn 3^x-2^y-2015^z=85
Cho các số x, y, z là các số hữu tỉ thỏa mãn điều kiện: xyz = 1; x/y3 + y/z3 + z/x3 = x3/z + y3/x + z3/y. Chứng minh rằng trong 3 số x, y, z tồn tại ít nhất 1 số là lập phương của một số hữu tỉ còn lại.
Chứng minh rằng không tồn tại số hữu tỉ x,y thoả mãn: x2 + y2=3
Cho x, y, z là các số hữu tỉ thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{z}\)
Chứng minh rằng \(\sqrt{x^2+y^2+z^2}\) là số hữu tỉ
Các idol dô đây lẹ
Chứng minh rằng không tồn tại x,y,z sao cho | x - 2y | + | 4y - 5z | + | z - 3x | = 2011
Chứng minh rằng: \(\dfrac{5x^3-y^3}{3x^2+xy}\)+\(\dfrac{5y^3-z^3}{3y^2+yz}\)+\(\dfrac{5z^3-x^3}{3z^2+xz}\)<=x+y+z, với z,y,z>0
Để chứng minh bất đẳng thức trên, ta sẽ sử dụng phương pháp giả sử ngược (Proof by Contradiction). Giả sử bất đẳng thức trên không đúng, tức là: (5x^3 - y^3)/(3x^2 + xy + 5y^3) + (5y^3 - z^3)/(3y^2 + yz + 5z^3) + (5z^3 - x^3)/(3z^2 + xz + 5x^3) > x + y + z Ta có thể viết lại bất đẳng thức trên thành: (5x^3 - y ^3)/(3x^2 + xy + 5y^3) - x + (5y^3 - z^3)/(3y^2 + yz + 5z^3) - y + (5z^3 - x^3 )/(3z^2 + xz + 5x^3) - z > 0 Tiếp theo, ta nhận thấy rằng với mọi a, b > 0, ta luôn có: (a^3 - b^3)/(a^2 + ab + b^2) - a > 0 and (a^3 - b^3)/(a^2 + ab + b^2) - b > 0. Vì vậy, áp dụng bất đẳng thức trên từng phần thức trong tổng, ta có: (5x^3 - y^3)/(3x^2 + xy + 5y^3) - x > 0 (5y ^3 - z^3)/(3y^2 + yz + 5z ^3) - y > 0 (5z^3 - x^3)/(3z^2 + xz + 5x^3) - z > 0 Khi đặt a = x^3, b = y^3, c = z^3, ta có: (5a - b)/(3a^2 + ab + 5b) - a^(1/3) > 0 (5b - c)/(3b^2 + bc + 5c) - b^(1/3) > 0 (5c - a)/(3c^2 + ac + 5a) - c^(1/3) > 0 Nói cách khác, ta có các bất đẳng thức sau: (5a - b)/(3a^2 + ab + 5b) > a^(1/3) (5b - c)/(3b^2 + bc + 5c) > b^(1/3) ( 5c - a)/(3c^2 + ac + 5a) > c^( 1/3) Áp dụng bất đẳng thức AM-GM, ta có: 3a^2 + ab + 5b ≥ 3∛(15a^2b) 3b^2 + bc + 5c ≥ 3∛(15b^2c) 3c^2 + ac + 5a ≥ 3∛(15c^2a) Khi đặt A = 3a^2 + ab + 5b, B = 3b^2 + bc + 5c, C = 3c^2 + ac + 5a, ta có: A > a ^ (1/3) B > b^(1/3) C > c^(1/3) Từ đó, ta có: (A + B + C) > (a^(1/3) + b^(1/3) + c^(1/3)) Nhưng A, B, C lần lượt tương ứng với các số mẫu trong bất đẳng thức ban đầu, ta thu được: (5a - b)/(3a^2 + ab + 5b) + (5b - c)/(3b^2 + bc + 5c) + (5c - a)/(3c^ 2 + ac + 5a) > (a^(1/3) + b^(1/3) + c^(1/3)) Tuy nhiên, điều này trái với giả định ban đầu.
Đúng 0
Bình luận (0)