cho tam giác ABC cân tại A ( AB = AC ) D thuộc AB; E thuộc AC sao cho AD= AE. Gọi M là trung điểm của BC
a,Chứng minh DE//BC b, tam giác MBD= tam giác MCE c, tam giác AMD= tam giác AME
TL
Những câu hỏi liên quan
Cho tam giác ABC cân tại A (góc A < 90 độ).Kẻ BM vuông tại AC (M thuộc AC) , CD vuông tại AB (D thuộc AB). BM và CD cắt nhau tại E.
a, Chứng minh tam giác BDC = tam giác CMD
b, Chứng minh tam giác BCE cân
a. Xét \(2\Delta:\Delta BDC\) và \(\Delta CMD\) có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\left(gt\right)\\BC.chung\end{matrix}\right.\)
\(\Rightarrow\Delta BDC=\Delta CMD\) (cạnh huyền - góc nhọn)
b. Vì \(\Delta BDC=\Delta CMD\) (theo câu a)
\(\Rightarrow\widehat{DCB}=\widehat{MBC}\) (2 góc tương ứng)
\(\Rightarrow\Delta BCE\) cân tại E
Đúng 3
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
Bài 3:Cho tam giác ABC cân tại A. Có BD và CE là hai đường trung điểm; D thuộc AC, E thuộc AB. Chứng minh rằng
a)Tam giác ADE cân tại A
b)Tam giác ABD = Tam giác ACE
c)BCDE là hình thang cân
a) Ta có: \(AD=DC=\dfrac{AC}{2}\)(D là trung điểm của AC)
\(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
mà AC=AB(ΔBAC cân tại A)
nên AD=DC=AE=EB
Xét ΔADE có AE=AD(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔADB và ΔAEC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
AD=AE(cmt)
Do đó: ΔADB=ΔAEC(c-g-c)
c) Ta có: ΔAED cân tại A(gt)
nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAED cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên ED//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Xét tứ giác BCDE có ED//BC(cmt)
nên BCDE là hình thang có hai đáy là ED và BC(Định nghĩa hình thang)
Hình thang BCDE(ED//BC) có BD=EC(ΔADB=ΔAEC)
nên BCDE là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a có ab = ac =5cm bc=8cm kẻ ah vuông góc với bc (H thuộc B) b) Kẻ HD vuông góc với AB (D thuộc AB) ;HE vuông góc với AC (E thuộc AC) . CMR Tam giác HDE là tam giác cân
b) Xét ΔBAH vuông tại H và ΔCAH vuông tại H có
BA=CA(ΔBAC cân tại A)
AH chung
Do đó: ΔBAH=ΔCAH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔDHB vuông tại D và ΔEHC vuông tại E có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔDHB=ΔEHC(Cạnh huyền-góc nhọn)
Suy ra: HD=HE(Hai cạnh tương ứng)
Xét ΔHDE có HD=HE(cmt)
nên ΔHDE cân tại H(Định nghĩa tam giác cân)
Đúng 2
Bình luận (0)
câu a đâu rồi bạn ơi ???
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A có AB=AC=5cm.Gọi M là điểm thuộc cạnh BC, kẻ MD//AC (D thuộc AB), ME//AB ( E thuộc AC). Tính chu vi tứ giác ADME
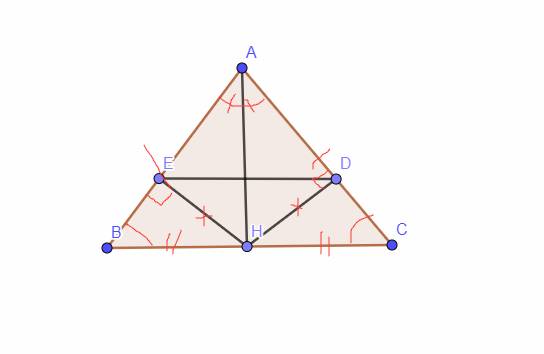
cho tam giác cân ABC cân tại A. Gọi H là trung điểm BC. a. chứng minh góc BAH = góc CAH. b. Kẻ HE vuông góc AB (E thuộc AB). Kẻ HD vuông góc AC (D thuộc AC). Chứng minh HDE là tam giác cân
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `BAH` và Tam giác `CAH` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`HB = HC ( H` là trung điểm của `BC)`
`=> \text {Tam giác BAH = Tam giác CAH (c-g-c)}`
`->`\(\widehat{BAH}=\widehat{CAH} (\text {2 góc tương ứng})\)
`b,` Xét Tam giác `HEA` và Tam giác `BDA` có:
`AH` chung
\(\widehat{EAH}=\widehat{DAH} (a)\)
\(\widehat{HEA}=\widehat{HDA}=90^0\)
`=> \text {Tam giác HEA = Tam giác BDA (ch-gn)}`
`-> HE = HD (\text {2 cạnh tương ứng})`
`\text {Xét Tam giác HDE: HD = HE} -> \text {Tam giác HDE cân tại H}`
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A . gọi M là trung điểm của BC . kẻ BD vuông góc với AC , CE vuông góc với AB ( D thuộc AC ; E thuộc AB ) . BD cắt CE tại I . chứng minh : BE = CD và tam giác IBC cân
Xem chi tiết
Cho tam giác ABC cân tại A,các đường cao BD,CE (D thuộc AC,E thuộc AB).Chứng minh
a)Tam giác BDC= tam giác CEB
b)Tứ giác BEDC là hình thang cân
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
b: ΔEBC=ΔDCB
=>EB=DC
AE+EB=AB
AD+DC=AC
mà EB=DC và AB=AC
nên AE=AD
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
Hình thang BEDC có \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
Đúng 1
Bình luận (0)
cho tam giác ABC vuông cân tại A. Dựng tam giác DEF vuông cân tại D có D thuộc AB, E thuộc AC, F thuộc BC. chứng minh: \(_{S_{DEF}=\frac{1}{5}S_{ABC}}\)
Cho tam giác ABC cân tại A,AB=4.Từ 1 điểm D trên cạnh BC vẽ DE//AB (E thuộc AC) và DF//AC (F thuộc AB) tính chu vi tứ giác AEDF
Lời giải:
$DF\parallel AE, DE\parallel AF$ nên $AEDF$ là hình bình hành
$P_{AEDF}=AE+DF+DE+AF$
Lại có:
$DF\parallel AC$ nên áp dụng định lý Talet:
$\frac{DF}{AC}=\frac{BF}{AB}$. Mà $AB=AC$ nên $DF=BF$
$DE\parallel AB$ nên áp dụng định lý Talet:
$\frac{CE}{AC}=\frac{DE}{AB}$ mà $AB=AC$ nên $CE=DE$
Do đó:
$P_{AEDF}=AE+BF+CE+AF=(AE+CE)+(BF+AF)=AC+AB=4+4=8$ (cm)
Đúng 2
Bình luận (0)





