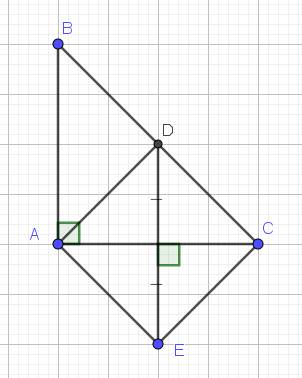
Cho tam giác ABC với đường cao AH và các điểm D;E sao cho AB;AC thứ tự là các đường trung trực của đoạn HD, HE. Gọi M;N lần lượt là giao điểm của DE với AB và AC
Chứng minh: AH,BN,CM đồng quy
Bạn nào trả lời nhanh mình lấy 6 nick hoc24 của mình tick cho (cả nick này nữa)


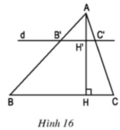

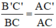
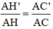
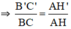
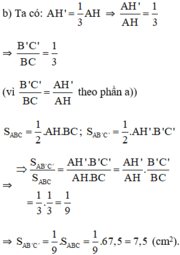
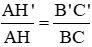 .
.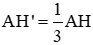 và diện tích tam giác ABC là 67,5 cm
và diện tích tam giác ABC là 67,5 cm