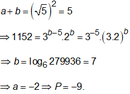tính giá trị biểu thức a2b-a3-9b+9a biết a=-3 b=-2
TB
Những câu hỏi liên quan
Cho a, b, c, d là các số thực thỏa mãn 0 ≤ a, b, c ≤ 1. Tìm giá trị lớn nhất của biểu thức T = 2( a3 + b3 + c3 ) – ( a2b + b2c + c2a ).
Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)
Đúng 1
Bình luận (1)
Cho hai số thực
a
,
b
phân biệt thỏa mãn
log
3
7
-
3
a
2
-
a
và
log
3
7
-
3
b
2
-
b
Giá trị biểu thứ...
Đọc tiếp
Cho hai số thực a , b phân biệt thỏa mãn log 3 7 - 3 a = 2 - a và log 3 7 - 3 b = 2 - b Giá trị biểu thức 9 a + 9 b bằng
A.67
B.18
C.31
D.82
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
Câu 5:
\(D\left(2\right)=21a+9b-6a-4b\)
\(D\left(2\right)=\left(21a-6a\right)+\left(9b-4b\right)\)
\(D\left(2\right)=15a+5b\)
Mà: \(3a+b=18\Rightarrow b=18-3b\)
\(\Rightarrow D\left(2\right)=15a+5\left(18-3b\right)\)
\(D\left(2\right)=15a+90-15a\)
\(D\left(2\right)=90\)
Vậy: ...
Đúng 2
Bình luận (3)
Câu 4:
\(D\left(1\right)=4a+10b-b+2a\)
\(D\left(1\right)=\left(4a+2a\right)+\left(10b-b\right)\)
\(D\left(1\right)=6a+9b\)
Mà: \(2a+3b=12\Rightarrow a=\dfrac{12-3b}{2}\)
\(\Rightarrow D\left(1\right)=6\left(\dfrac{12-3b}{2}\right)+9b\)
\(D\left(1\right)=\dfrac{6\left(12-3b\right)}{2}+9b\)
\(D\left(1\right)=3\left(12-3b\right)+9b\)
\(D\left(1\right)=36-9b+9b\)
\(D\left(1\right)=36\)
Vậy: ...
Đúng 2
Bình luận (0)
Câu 3:
Sửa đề: \(C=5a-4b+7a-8b\)
\(C=\left(5a+7a\right)-\left(4b+8b\right)\)
\(C=12a-12b\)
\(C=12\left(a-b\right)\)
\(C=12\cdot8\)
\(C=96\)
Vậy: ...
Đúng 2
Bình luận (0)
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
4:
D=6a+9b=3(2a+3b)=36
5:
D=15a+5b=5(3a+b)=90
Đúng 0
Bình luận (0)
Câu 3: Tính giá trị của biểu thức C 5a − 4b + 7a + 8 . Biết a-b8.
Câu 4: Tính giá trị của biểu thức D 4a + 10b - b+ 2a. Biết 2a+3b12
Câu 5: Tính giá trị của biểu thức D21a + 9b — 6a — 4b. Biết 3a+b18
Đọc tiếp
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
Cho các số thực a, b đồng thời thỏa mãn
3
-
a
2
b
1152
và
log
5
(
a
+
b
)
...
Đọc tiếp
Cho các số thực a, b đồng thời thỏa mãn 3 - a 2 b = 1152 và log 5 ( a + b ) = 2 . Tính giá trị biểu thức P = a - b.
Cho ba số thực dương a; b và c thỏa mãn :\(a+b+c=3\). Tìm giá trị lớn nhất của biểu thức sau:
\(P=\sqrt{9a+16b}+\sqrt{9b+16c}+\sqrt{9c+16a}\)
\(P\le\sqrt{3\left(9a+16b+9b+16c+9c+16a\right)}=\sqrt{75\left(a+b+c\right)}=15\)
\(P_{max}=15\) khi \(a=b=c=1\)
Đúng 2
Bình luận (2)
Rút gọn rồi tính giá trị các biểu thức sau:
a
)
−
9
a
−
9
+
12
a
+
4
a
2
t
a
i
...
Đọc tiếp
Rút gọn rồi tính giá trị các biểu thức sau:
a ) − 9 a − 9 + 12 a + 4 a 2 t a i a = − 9 b ) 1 + 3 m m − 2 m 2 − 4 m + 4 tai m = 1 , 5 c ) 1 − 10 a − 25 a 2 − 4 a t a i a = 2 d ) 4 x − 9 x 2 + 6 x + 1 t a i x = − 3
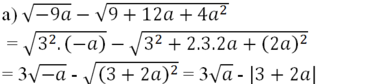
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
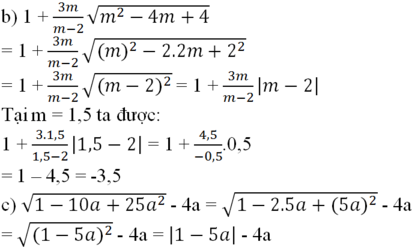
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
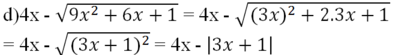
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1|
= -4√3 - |-3√3 + 1|
= -4√3 - (3√3 - 1)
= -7√3 + 1
Đúng 0
Bình luận (0)
Cho 3 số thực dương a, b, c thoả mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức:
\(P=\frac{a}{9a^3+3b^2+c}+\frac{b}{9b^3+3c^2+a}+\frac{c}{9c^3+3a^2+b}\)
Áp dụng BĐT Bunhiacopxky :
\(\left(9a^3+3b^2+c\right)\left(\frac{1}{9a}+\frac{1}{3}+c\right)\ge\left(a+b+c\right)^2=1\)
\(\Rightarrow9a^3+3b^2+c\ge\frac{1}{\frac{1}{9a}+\frac{1}{3}+c}\)
\(\Rightarrow\frac{a}{9a^3+3b^2+c}\le a\left(\frac{1}{9a}+\frac{1}{3}+c\right)\)
Thực hiện tương tự với các phân thức khác và cộng theo vế :
\(P\le\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{a+b+c}{3}+\left(ab+bc+ac\right)\)
\(P\le\frac{2}{3}+ab+bc+ac\)
Theo hệ quả quen thuộc của BĐT AM - GM :
\(ab+bc+ac\le\frac{\left(a+b+c\right)^2}{3}=\frac{1}{3}\)
\(\Rightarrow P\le\frac{2}{3}+\frac{1}{3}=1\Rightarrow P_{max}=1\)
Vậy GTLN của P là 1 khi \(a=b=c=\frac{1}{3}\)