Cho ΔABC cân tại A,đường cao AD.Biết AB=10cm;BC=12cm.
a.Tính độ dài các đoạn thẳng BD,AD
b.Gọi G là trọng tâm của ΔABC.Chứng minh rằng 3 điểm A,G,D thẳng hàng.
c.Chứng minh ΔABG=ΔACG
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho ΔABC cân tại có đường cao AH
a) CM ΔAHB=ΔACH và AH là tia p/g của góc BAC
b) Cho BH=8cm; AB=10cm. Tính AH
a) Xét tam giác AHB vuông tại H và tam giác AHC vuông tại C:
AH chung.
AB = AC (Tam giác ABC cân tại A).
=> Tam giác AHB = Tam giác AHC (cạnh huyền - cạnh góc vuông).
Xét tam giác ABC cân tại A: AH là đường cao (gt).
=> AH là phân giác \(\widehat{BAC}\) (Tính chất tam giác cân).
b) Xét tam giác ABH vuông tại H:
Ta có: \(AB^2=AH^2+BH^2\) (Định lý Pytago).
Thay số: \(10^2=AH^2+8^2.\Rightarrow AH=\sqrt{10^2-8^2}=\sqrt{36}=6\left(cm\right).\)
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AH chung
AB=AC
Do đó: ΔAHB=ΔAHC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
b: XétΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=6(cm)
Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
Cho ΔABC cân tại A có BC = 5cm, B = C = 40°, Tính AB và đường cao AH
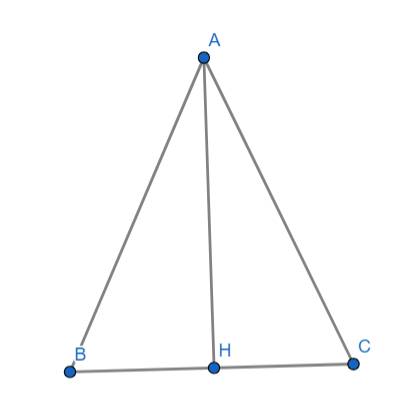
Do tam giác ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến nên:
\(BH=CH=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Xét tam giác vuông ABH ta có:
\(sinB=\dfrac{BH}{AB}\)
\(\Rightarrow sin40^{o0}=\dfrac{2,5}{AB}\Rightarrow AB=\dfrac{2,5}{sin40^o}\approx4\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác đó ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{4^2-2,5^2}\approx3\left(cm\right)\)
Cho ΔABC vuông tại A , đường cao AH ( H∈BC). Biết AC = 8cm, BC =10cm . Tính độ dài các đoạn thẳng AB, BH , CH và AH
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=10^2-8^2=36\)
hay AB=6(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AB\cdot AC=AH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{36}{10}=3.6\left(cm\right)\\CH=\dfrac{64}{10}=6.4\left(cm\right)\\AH=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\end{matrix}\right.\)
Cho ΔABC cân tại A, đường trung tuyển AD a, Chứng minh ΔABD = ΔACD b, Chứng minh AD BC c, Cho AB = AC = 10cm ; BC = 8cm . Tính AM d, Kẻ trung tuyến CG . Chứng minh DG // AC
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABC cân tại A
mà AD là trung tuyến
nên AD vuông góc BC
d: DG là đường trung bình
=>DG//AC
Cho ΔABC cân tại A có AB =AC =13cm ,BC =10cm .Tính cos góc A.
Từ A kẻ đường cao AH vuông góc với BC tại H.
Từ B kẻ đường cao BK vuông góc với AC tại K
Khi đó, ta có BH = HC = 1/2BC = 5 (cm)
\(AH=\sqrt{AC^2-\left(\frac{BC}{2}\right)^2}=13^2-5^2=12\left(cm\right)\)
Dễ thấy hai tam giác HCA và KCB đồng dạng (g.g)
Suy ra \(\frac{HC}{KC}=\frac{AC}{BC}\) hay \(\frac{5}{KC}=\frac{13}{10}\Rightarrow KC=\frac{50}{13}\Rightarrow AK=AC-KC=13-\frac{50}{13}=\frac{119}{13}\left(cm\right)\)
Xét tam giác AKB, ta có :
\(CosA=\frac{AK}{AC}=\frac{\frac{119}{13}}{13}=\frac{119}{169}\)
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
Kẻ AH vuông góc với BC.
Vì ABC là tam giác cân nên AH là trung tuyến ứng với BC.
=> HB = HC = BC/2 = 10/2=5 cm.
cos C = 5/13 => Góc C = 67 độ 38 phút.
Vì ABC là tam giác cân nên góc B = Góc C = 67 độ 23 phút.
=> Góc A = 180 - 2 . 67 độ 23 phút = 45 độ 14 phút
=> cos A = 119/169
ΔABC vuông tại A, AB<AC, đường cao AH dài 4cm, BC=10cm. Tính \(\frac{AB}{AC}\)
Xét ΔABC vuông tại A có
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
\(\Leftrightarrow\dfrac{1}{100-AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{16}\)
\(\Leftrightarrow\dfrac{AC^2+100-AC^2}{AC^2\left(100-AC^2\right)}=\dfrac{1}{16}\)
\(\Leftrightarrow100AC^2-AC^4=1600\)
\(\Leftrightarrow AC^4-100AC^2+1600=0\)
\(\Leftrightarrow AC^4-80AC^2-20AC^2+1600=0\)
\(\Leftrightarrow\left(AC^2-80\right)\left(AC^2-20\right)=0\)
=>\(AC=2\sqrt{5}\left(cm\right)\)
=>\(AB=4\sqrt{5}\left(cm\right)\)
=>AB/AC=2
Cho tam giác ABC vuông tại A , đường cao AH
a) Chứng minh ΔABC ∼ ΔABH
b)Vẽ tia phân giác AI . Tính IB và IC biết BC =10cm và AB\AC=2\3
Cho ΔABC cân tại A. Qua A kẻ đường thẳng vuông góc vói BC, cắt BC tại H. Gọi M và N lần lượt là trung điểm của AC và AB
a) C.minh ΔAHB = ΔAHC
b) Tính độ dài AH bt AB = AC = 10cm, BC = 12cm
c) C.minh MN//BC
d) C.minh ΔGBC cân tại G
e) Gọi G là giao điểm của BM và CN. C.minh 3 điểm A, G, H thẳng hàng
_Vẽ hộ hình, cảm ơn
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔAHB=ΔAHC
nên HB=HC
=>HB=BC/2=6(cm)
Xét ΔAHB vuông tại H có
\(AB^2=AH^2+BH^{ }\)
hay AH=8(cm)
c: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình
=>MN//BC
d: Xét ΔNCB và ΔMBC có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó: ΔNCB=ΔMBC
Suy ra: \(\widehat{GCB}=\widehat{GBC}\)
hay ΔGBC cân tại G