B= x + \(\dfrac{1}{x}\)với x > hoặc bằng 2
Tìm GTNN
PHƯƠNG PHÁP ĐIỂM DƠI
C= x + \(\dfrac{1}{x}\) với x > hoặc bằng 4
Tìm GTNN
PHƯƠNG PHÁP ĐIỂM DƠI
\(C=\dfrac{1}{x}+\dfrac{x}{16}+\dfrac{15}{16}x\ge2\sqrt{\dfrac{1}{x}.\dfrac{x}{16}}+\dfrac{15}{16}.4=\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
dấu = xảy ra khi x=4
\(x+\dfrac{1}{x}=\dfrac{1}{16}x+\dfrac{1}{x}+\dfrac{15}{16}x\ge2\sqrt{\dfrac{x}{16x}}+\dfrac{15}{16}.4=\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
\(minC=\dfrac{17}{4}\Leftrightarrow x=4\)
\(C=x+\dfrac{1}{x}=\dfrac{x}{16}+\dfrac{1}{x}+\dfrac{15x}{16}\ge2\sqrt{\dfrac{1}{16}}+\dfrac{15.4}{16}=\dfrac{17}{4}\)
dấu"=" xảy ra<=>x=4
A= \(x+\dfrac{1}{x}\) với 0 < x < hơn bằng \(\dfrac{1}{4}\)
Tìm GTNN
PHƯƠNG PHÁP ĐIỂM DƠI
\(A=x+\dfrac{1}{x}=x+\dfrac{1}{16x}+\dfrac{15}{16x}\ge2\sqrt{x.\dfrac{1}{16x}}+\dfrac{15}{16x}\ge\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)(do \(x\le\dfrac{1}{4}\Rightarrow\dfrac{15}{16x}\le\dfrac{15}{4}\))
\(minA=\dfrac{17}{4}\Leftrightarrow x=\dfrac{1}{4}\)
A= \(A=-\dfrac{x}{4-x}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\) với x lớn hơn hoặc bằng 0; x khác 4
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
a. Rút gọn A
b. Tính giá trị của A khi x=36
c. Tìm x để a=-1/3
d. tìm x nguyên để biểu thức A có giá trị nguyên
e. Tìm x để A:B =-2
F. Tìm x để A đạt giá trị nhỏ nhất, tính giá trị nhỏ nhất
mn giúp mình với ạ mình đang cần gấp mình cảm ơn
cho biểu thức A=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\)-\(\dfrac{2}{\sqrt{x}-1}\)-\(\dfrac{2}{x-1}\)( với x> hoặc bằng 0, x khác 1) và B=\(\dfrac{\sqrt{x}-1}{\sqrt{x}}\) ( với x >0)
a) Rút gòn a ( ko cần làm vì mk làm rùi)
b) Tính giá trị của B khi \(^{4x^2+x-5=0}\)
c) Tìm m để có giá trị x thỏa mãn 2A+mB=0
Giúp mk b với c với
b) Ta có: \(4x^2+x-5=0\)
\(\Leftrightarrow4x^2-4x+5x-5=0\)
\(\Leftrightarrow4x\left(x-1\right)+5\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\4x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{5}{4}\left(loại\right)\end{matrix}\right.\)
Thay x=1 vào biểu thức \(B=\dfrac{\sqrt{x}-1}{\sqrt{x}}\), ta được:
\(B=\dfrac{\sqrt{1}-1}{\sqrt{1}}=0\)
Vậy: Khi \(4x^2+x-5=0\) thì B=0
Bài 1 : cho biểu thức
\(p=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\) với x lớn hơn hoặc bằng 0 ; x # 1
1) rút gọ P
2 tìm x để P = \(\dfrac{7}{4}\)
tìm giá trị nhỏ nhất của p
1, Với \(x\ge0,x\ne1\) ta có :
\(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{x-1}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2, Ta có \(P=\dfrac{7}{4}\)
\(\Rightarrow\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}=\dfrac{7}{4}\)
\(\Leftrightarrow4\left(2\sqrt{x}+1\right)=7\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow8\sqrt{x}+4=7\sqrt{x}=7\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\left(tm\right)\)
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\left(\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-1}\right)\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}-\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Để \(P=\dfrac{7}{4}\) thì \(\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}=\dfrac{7}{4}\)
\(\Leftrightarrow4\cdot\left(2\sqrt{x}+1\right)=7\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow8\sqrt{x}+4=7\sqrt{x}+7\)
\(\Leftrightarrow8\sqrt{x}-7\sqrt{x}=7-4\)
\(\Leftrightarrow\sqrt{x}=3\)
hay x=9(nhận)
Vậy: Để \(P=\dfrac{7}{4}\) thì x=9
Cho P = \(\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}\) ( x lớn hơn hoặc bằng 0, x khác 1) Tìm x để P lớn hơn hoặc bằng 1
Để \(P\ge1\) thì \(P-1\ge0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-1-\sqrt{x}+1}{\sqrt{x}-1}\ge0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-1>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x>1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được: x=0 hoặc x>1
A=\(2\sqrt{20}-\dfrac{2}{\sqrt{3}+1}-\sqrt{80}+\sqrt{4+2\sqrt{3}}\)
B=\(\left(1+\dfrac{x+\sqrt{x}}{1+\sqrt{x}}\right)\left(1+\dfrac{x-\sqrt{x}}{1-\sqrt{x}}\right)\) (0 nhỏ hơn hoặc bằng x; x khác 1)
a) Rút gọn A, B
b) Tìm giá trị của x đề A=4\(\sqrt{B}\)
Help meeeeeeeeeeee
\(a,A=2\sqrt{20}-\dfrac{2}{\sqrt{3}+1}-\sqrt{80}+\sqrt{4+2\sqrt{3}}\\ =2.2\sqrt{5}-\dfrac{2\left(\sqrt{3}-1\right)}{\sqrt{3^2}-1}-4\sqrt{5}+\sqrt{\left(\sqrt{3}+1\right)^2}\\ =-\dfrac{2\left(\sqrt{3}-1\right)}{2}+\left|\sqrt{3}+1\right|\\ =-\sqrt{3}+1+\sqrt{3}+1\\ =2\)
\(B=\left(1+\dfrac{x+\sqrt{x}}{1+\sqrt{x}}\right)\left(1+\dfrac{x-\sqrt{x}}{1-\sqrt{x}}\right)\left(dk:x\ge0,x\ne1\right)\\ =\left(1+\dfrac{\sqrt{x}\left(1+\sqrt{x}\right)}{1+\sqrt{x}}\right)\left(1-\dfrac{\sqrt{x}\left(1-\sqrt{x}\right)}{1-\sqrt{x}}\right)\\ =\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)\\ =1-x\)
\(b,A=4\sqrt{B}\Leftrightarrow4\sqrt{1-x}=2\\ \Leftrightarrow\sqrt{1-x}=\dfrac{1}{2}\\ \Leftrightarrow\left|1-x\right|=\dfrac{1}{4}\)
\(\Leftrightarrow1-x=\dfrac{1}{4}\\ \Leftrightarrow x=\dfrac{3}{4}\left(tm\right)\)
Vậy \(x=\dfrac{3}{4}\) thì \(A=4\sqrt{B}\).
a) \(A=2\sqrt{20}-\dfrac{2}{\sqrt{3}+1}-\sqrt{80}+\sqrt{4+2\sqrt{3}}\)
\(A=2\cdot2\sqrt{5}-\dfrac{2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-4\sqrt{5}+\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}\cdot1+1^2}\)
\(A=4\sqrt{5}-\dfrac{2\left(\sqrt{3}-1\right)}{2}-4\sqrt{5}+\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(A=-\left(\sqrt{3}-1\right)+\sqrt{3}+1\)
\(A=-\sqrt{3}+1+\sqrt{3}+1\)
\(A=2\)
\(B=\left(1+\dfrac{x+\sqrt{x}}{1+\sqrt{x}}\right)\left(1+\dfrac{x-\sqrt{x}}{1-\sqrt{x}}\right)\)
\(B=\left[1+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right]\left[1-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right]\)
\(B=\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)\)
\(B=1^2-\left(\sqrt{x}\right)^2\)
\(B=1-x\)
b) Ta có: \(A=4\sqrt{B}\)
\(\Rightarrow2=4\sqrt{1-x}\)
\(\Leftrightarrow\sqrt{1-x}=\dfrac{1}{2}\)
\(\Leftrightarrow1-x=\dfrac{1}{4}\)
\(\Leftrightarrow x=1-\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{3}{4}\left(tm\right)\)
Cho 2 hàm số y= 2x-3 (d1) và y= \(\dfrac{1}{2}\)x+3 (d2)
a, Vẽ đths y= 2x-3 trên hệ toạ trục Oxy
b, Gọi giao điểm của 2 đường thẳng (d1) và (d2) là M. Tìm toạ độ điểm M bằng phương pháp đại số
GIÚP MÌNH VỚI
a: 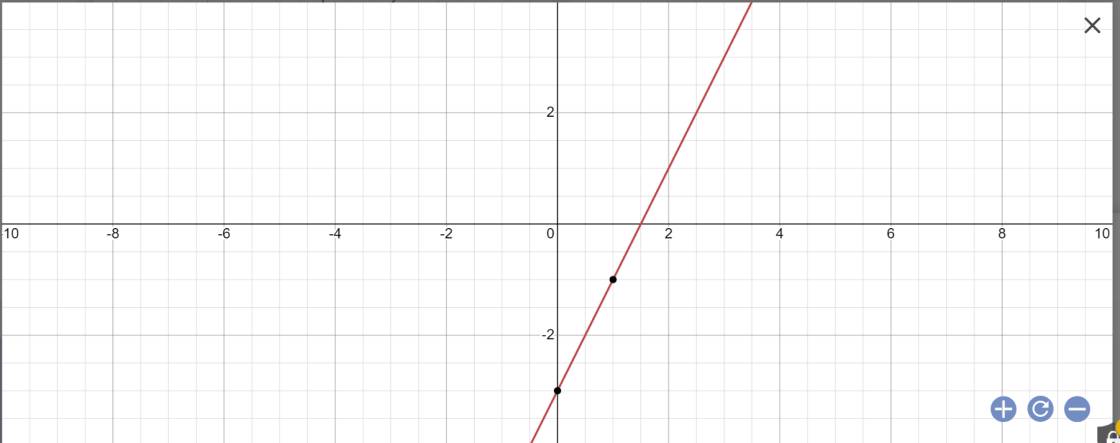
b: Phương trình hoành độ giao điểm là:
\(2x-3=\dfrac{1}{2}x+3\)
=>\(2x-\dfrac{1}{2}x=3+3=6\)
=>\(\dfrac{3}{2}x=6\)
=>\(x=6:\dfrac{3}{2}=4\)
Thay x=4 vào y=2x-3, ta được:
\(y=2\cdot4-3=5\)
Vậy: M(4;5)
Cho P = \(\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}\) (đk x>-0 ; x khác 1/2 )
TÌM X BT |P| > HOẶC BẰNG P
Thấy : \(\sqrt{x}\ge0\)
\(\Rightarrow P=\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}>0\)
\(\Rightarrow\left|P\right|=P\)
Ta có : \(\left|P\right|=P\ge P\)
=> P = P .
Vậy \(\forall x>0\) TMYC đè bài
Ơ câu này giống câu ở dưới thế ?_? Lặp câu hỏi à bạn :v
Ta có: \(\left|P\right|\ge P\)
\(\Leftrightarrow\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}\ge0\)
\(\Leftrightarrow x>0\)