Cần gấp câu f ạ
LY
Những câu hỏi liên quan
cần gấp ạ câu d , e , f, g, h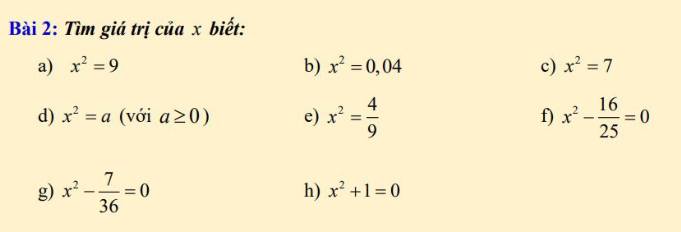
d) \(x^2=a\left(a\ge0\right)\)
\(\Rightarrow x=\sqrt{a}\)
e) \(x^2=\dfrac{4}{9}\)
\(\Rightarrow x^2=\left(\pm\dfrac{2}{3}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f) \(x^2-\dfrac{16}{25}=0\)
\(\Rightarrow x^2=\dfrac{16}{25}\)
\(\Rightarrow x^2=\left(\pm\dfrac{4}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
g) \(x^2-\dfrac{7}{36}=0\)
\(\Rightarrow x^2=\dfrac{7}{36}\)
\(\Rightarrow x^2=\left(\pm\sqrt{\dfrac{7}{36}}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{7}{36}}\\x=-\sqrt{\dfrac{7}{36}}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{7}}{6}\\x=-\dfrac{\sqrt{7}}{6}\end{matrix}\right.\)
h) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow x^2+1\ge1>0\forall x\)
mà \(x^2+1=0\)
nên không tìm được giá trị nào của x thoả mãn đề bài.
Đúng 2
Bình luận (0)
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mọi người giúp mk giải câu này vs ạ,
Cho hàm số y = f(x) = x -2
a)Tính f(-1) ; f(0)
b)Tìm x để f(x) = 3
mk đg cần gấp ![]()
a: f(-1)=-03
f(0)=-2
b: f(x)=3
=>x-2=3
hay x=5
Đúng 0
Bình luận (1)
Cho tam giác DEF, kẻ DI vuông góc EF tại F . Biết DF = 20cm ,DI=12cm , EI = 9cm
a)tính độ dài cạnh IF, ED và chu vi tam giác.
b) CM tam giác DEF là tg vuông
Ko cần giải câu a đâu ạ , tui cần gấp câu b🙆♀️❤
Xem chi tiết
Ai giúp với ạ cần gấp câu trả lời gấp ạ
giải giúp câu này với ạ, cần giải rõ ràng dễ hiểu với ạ, cần gấp câu này😔
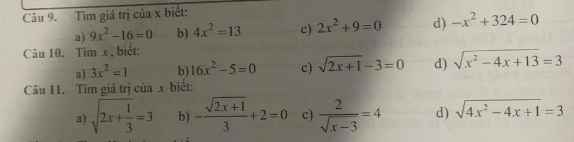
mình cần từ câu 9 đến 11 ạ mình cần gấp ạ cảm ơn
Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giúp mk câu 3 và câu 4 với ạ , mk cần gấp lắm ạ 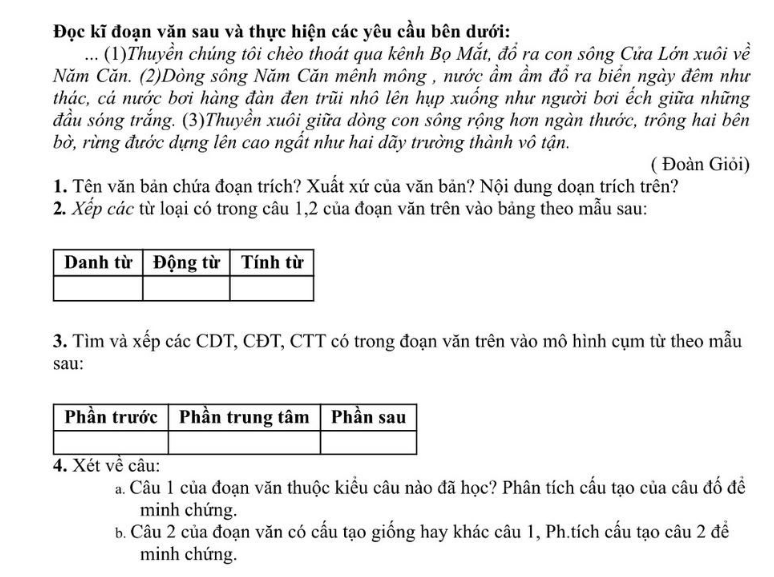
 em cần giải gấp câu b,c theo hệ thức lượng cần gấp ạ
em cần giải gấp câu b,c theo hệ thức lượng cần gấp ạ
b)\(\Delta DBC\) vuông tại B có đường cAO BA nên
\(\dfrac{1}{AB^2}=\dfrac{1}{BD^2}+\dfrac{1}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BD^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Leftrightarrow BD=\dfrac{15}{4}\left(cm\right)\)
\(AD=\sqrt{BD^2-AB^2}=\dfrac{9}{4}\left(cm\right)\)
c)\(\Delta ABD\) vuông tại A có đường cao AF nên
\(BF.BD=AB^2\left(1\right)\)
\(\Delta BAC\) vuông tại có đường cao AE nên
\(BE.BC=AB^2\left(2\right)\)
từ \(\left(1\right)và\left(2\right)\Rightarrow BF.BD=BE.BC\)
Đúng 1
Bình luận (0)





