Cho x+y+4=0. Tìm GTNN của:
P=\(2.\left(x^3+y^3\right)+3.\left(x^2+y^2\right)+16xy\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
tìm số nguyên dương x,y sao cho :\(x^3+y^3+4\left(x^2+y^2\right)+4\left(x+y\right)=16xy\)
\(pt=\left(x^3-4x^2+4x\right)+\left(y^3-4y^2+4y\right)+\left(8x^2+8y^2-16xy\right)=0\)
\(\Leftrightarrow x\left(x-2\right)^2+y\left(y-2\right)^2+8\left(x-y\right)^2=0\left(1\right)\)
Do \(x\left(x-2\right)^2\ge0,y\left(y-2\right)^2\ge0,8\left(x-y\right)^2\ge0\left(2\right)\)
Từ (1) và (2) =>x=y=2
Cho x,y>0 và xy=4.Tìm GTNN của \(Q=\dfrac{x^3}{4\left(y+2\right)}+\dfrac{y^3}{4\left(x+2\right)}\)
\(\dfrac{x^3}{4\left(y+2\right)}+\dfrac{x\left(y+2\right)}{16}\ge\dfrac{x^2}{4}\) ; \(\dfrac{y^3}{4\left(x+2\right)}+\dfrac{y\left(x+2\right)}{16}\ge\dfrac{y^2}{4}\)
\(\Rightarrow Q+\dfrac{2xy+2x+2y}{16}\ge\dfrac{x^2+y^2}{4}\ge\dfrac{\left(x+y\right)^2}{8}\)
\(\Rightarrow Q\ge\dfrac{\left(x+y\right)^2-\left(x+y\right)}{8}-\dfrac{1}{2}=\dfrac{\left(x+y-4\right)^2+7\left(x+y\right)-16}{8}-\dfrac{1}{2}\)
\(\Rightarrow Q\ge\dfrac{7\left(x+y\right)-16}{8}-\dfrac{1}{2}\ge\dfrac{14\sqrt{xy}-16}{8}-\dfrac{1}{2}=1\)
\(Q_{min}=1\) khi \(x=y=2\)
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Giải hệ phương trình : \(\left\{{}\begin{matrix}\left(x^2+y\right)^3+\left(y^2+x\right)^3=6\left(x^2-x\right)-6\left(y^2-y\right)\\8x^4+8y^4+8x^2+8y^2=9-16xy\left(x+y\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left(x+y\right)^2-\left(y^2-x\right)^3=6\left(x^2-x\right)-\left(y^2-y\right)\\8x^4+8y^4+8x^2+8y^2=9-16xy\left(x+y\right)\end{matrix}\right.\)
Help me giải hpt này với ạ
tìm nghiệp nguyên dương của phương trình
\(\left(x^3+y^3\right)+4\left(x^2+y^2\right)+4\left(x+y\right)=16xy\\\)
Ta có \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
Và \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow\left(a+b\right)^2\ge4ab\)
( dấu '=' xảy ra khi a=b)
Áp dụng các bđt trên ta có
\(x^3+y^3+4\left(x^2+y^2\right)+4\left(x+y\right)=x^3+y^3+4x^2+4y^2+4x+4y=x^3+4x^2+4x+y^3+4y^2+4y=x\left(x^2+4x+4\right)+y\left(y^2+4y+4\right)=x\left(x+2\right)^2+y\left(y+2\right)^2\ge x.8x+y.8y=8\left(x^2+y^2\right)\ge8.2xy=16xy\Leftrightarrow x^3+y^3+4\left(x^2+y^2\right)+4\left(x+y\right)\ge16\)
Dấu '=' xảy ra khi x=y=2
Vậy (x;y)=(2;2)
a,Cho x,y,z tm \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\x+y+z=4\end{matrix}\right.\). CM: \(-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b, cho \(x^2+3y^2=1\). Tìm GTLN, GTNN của\(P=x-y\)
c, Cho \(P=\dfrac{x^2-\left(x-4y\right)^2}{x^2+4y^2}\left(x^2+y^2>0\right)\)
Tìm GTLN của P
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Bài a hình như sai đề rồi bạn.
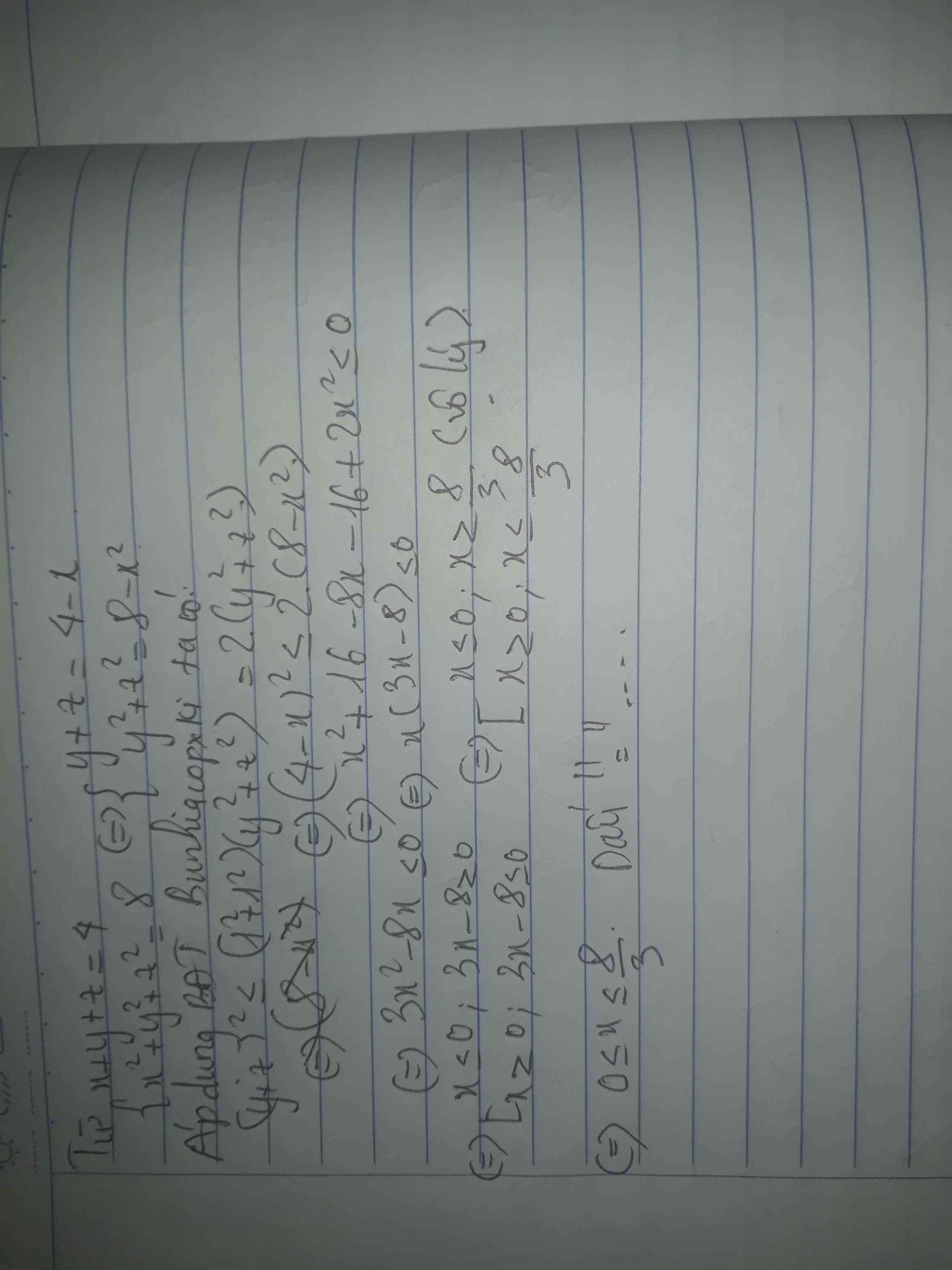
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
a, Cho x,y,z >0 thỏa điều kiện x+y+z=3. Tìm GTNN của A=\(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\)
b, cho x >1 , y>1. Tìm GTNN của A=\(\frac{\left(x^3+y^3\right)-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}\)
a,\(A\ge\frac{9}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\ge\frac{9}{\sqrt{3\left(x+y+z\right)}}=3\)=3
MInA=3<=>x=y=z=1
b)dùng cô si đi(đề thi chuyên bình phước năm 2016-2017)
Cho x,y,z>0 thỏa mãn: x+y+z=3. Tìm GTNN của \(P=\frac{\left(x+1\right)^2.\left(y+1\right)^2}{z^2+1}+\frac{\left(y+1\right)^2.\left(z+1\right)^2}{x^2+1}+\frac{\left(z+1\right)^2.\left(x+1\right)^2}{y^2+1}\)