\(\dfrac{2\sqrt{3}-10}{5}\cdot\sqrt{\dfrac{5+\sqrt{3}}{5-\sqrt{3}}}\)
MM
Những câu hỏi liên quan
thực hiện phép tính
A=\(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}+\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}\)
B=\(\sqrt{\dfrac{3-\sqrt{5}}{\sqrt{10}+\sqrt{2}}}\cdot\left(3+\sqrt{5}\right)\)
a) \(A=\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}+\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}\)
\(=\dfrac{2-\sqrt{3}}{1}+\dfrac{2+\sqrt{3}}{1}\)
=4
Đúng 0
Bình luận (0)
D sqrt{94-42sqrt{5}}-sqrt{94+42sqrt{5}}
A sqrt{sqrt{5}-sqrt{3-sqrt{29-12sqrt{5}}}}
C dfrac{2sqrt{4-sqrt{5+sqrt{21+sqrt{80}}}}}{sqrt{10}-sqrt{2}}
F sqrt{2+sqrt{3}}cdotsqrt{2+sqrt{2+sqrt{3}}cdotsqrt{2+sqrt{2+sqrt{2+sqrt{3}}}}}cdotsqrt{2-sqrt{2+sqrt{2+sqrt{3}}}}
B dfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{n-1}+sqrt{n}}
E dfrac{1}{sqrt{1}-sqrt{2}}-dfrac{1}{sqrt{2}-sqrt{3}}+dfrac{1}{sqrt{3}-sqrt{4}}-...-dfrac{1}{sqrt{24}-sqrt{25}}
Đọc tiếp
D = \(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\)
A = \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
C = \(\dfrac{2\sqrt{4-\sqrt{5+\sqrt{21+\sqrt{80}}}}}{\sqrt{10}-\sqrt{2}}\)
F = \(\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
B = \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{n-1}+\sqrt{n}}\)
E = \(\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-...-\dfrac{1}{\sqrt{24}-\sqrt{25}}\)
C = \(\dfrac{2\sqrt{4-\sqrt{5+\sqrt{21+\sqrt{80}}}}}{\sqrt{10}-\sqrt{2}}\)
C = \(\dfrac{2\sqrt{4-\sqrt{5+\sqrt{\left(\sqrt{20}+1\right)^2}}}}{\sqrt{10}-\sqrt{2}}\)
C = \(\dfrac{2\sqrt{4-\sqrt{6+\sqrt{20}}}}{\sqrt{10}-\sqrt{2}}\) = \(\dfrac{2\sqrt{4-\sqrt{\left(\sqrt{5}+1\right)^2}}}{\sqrt{10}-\sqrt{2}}\)
C = \(\dfrac{2\sqrt{3-\sqrt{5}}}{\sqrt{10}-\sqrt{2}}\) = \(\dfrac{2\sqrt{3-\sqrt{5}}\left(\sqrt{10}+\sqrt{2}\right)}{10-2}\)
C = \(\dfrac{2\sqrt{30-10\sqrt{5}}+2\sqrt{6-2\sqrt{5}}}{8}\)
C = \(\dfrac{2\sqrt{\left(5-\sqrt{5}\right)^2}+2\sqrt{\left(\sqrt{5}-1\right)^2}}{8}\)
C = \(\dfrac{2\left(5-\sqrt{5}\right)+2\left(\sqrt{5}-1\right)}{8}\)
C = \(\dfrac{10-2\sqrt{5}+2\sqrt{5}-2}{8}\) = \(\dfrac{8}{8}\) = \(1\)
Đúng 0
Bình luận (1)
D = \(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\)
D = \(\sqrt{\left(7-3\sqrt{5}\right)^2}-\sqrt{\left(7+3\sqrt{5}\right)^2}\)
D = \(7-3\sqrt{5}-\left(7+3\sqrt{5}\right)\) = \(7-3\sqrt{5}-7-3\sqrt{5}\)
D = \(-6\sqrt{5}\)
A = \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
A = \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}}\)
A = \(\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}\) = \(\sqrt{\sqrt{5}-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
A = \(\sqrt{\sqrt{5}-\sqrt{5}+1}\) = \(\sqrt{1}=1\)
Đúng 0
Bình luận (0)
1, dfrac{6-sqrt{6}}{sqrt{6}-1}+dfrac{6+sqrt{6}}{sqrt{6}}
2, dfrac{6-6sqrt{3}}{1-sqrt{3}}+dfrac{3sqrt{3}+3}{sqrt{3}+1}
3, dfrac{3+sqrt{3}}{sqrt{3}}+dfrac{sqrt{6}-sqrt{3}}{1-sqrt{2}}
4, dfrac{sqrt{15}-sqrt{12}}{sqrt{5}-2}+dfrac{6+2sqrt{6}}{sqrt{3}+sqrt{2}}
5, left(dfrac{3sqrt{125}}{15}-dfrac{10-4sqrt{5}}{sqrt{5}-2}right)cdotdfrac{1}{sqrt{5}}
Đọc tiếp
1, \(\dfrac{6-\sqrt{6}}{\sqrt{6}-1}+\dfrac{6+\sqrt{6}}{\sqrt{6}}\)
2, \(\dfrac{6-6\sqrt{3}}{1-\sqrt{3}}+\dfrac{3\sqrt{3}+3}{\sqrt{3}+1}\)
3, \(\dfrac{3+\sqrt{3}}{\sqrt{3}}+\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}\)
4, \(\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}+\dfrac{6+2\sqrt{6}}{\sqrt{3}+\sqrt{2}}\)
5, \(\left(\dfrac{3\sqrt{125}}{15}-\dfrac{10-4\sqrt{5}}{\sqrt{5}-2}\right)\cdot\dfrac{1}{\sqrt{5}}\)
1: \(=\sqrt{6}+\sqrt{6}+1=2\sqrt{6}+1\)
2: \(=\dfrac{6\left(1-\sqrt{3}\right)}{1-\sqrt{3}}+\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}+1}=6+3=9\)
3: \(=\sqrt{3}+1-\sqrt{3}=1\)
Đúng 0
Bình luận (0)
Bài 50 (trang 30 SGK Toán 9 Tập 1)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
$\dfrac{5}{\sqrt{10}}$; $\dfrac{5}{2 \sqrt{5}}$ ; $\dfrac{1}{3 \sqrt{20}}$ ; $\dfrac{2 \sqrt{2}+2}{5 \sqrt{2}}$ ;$\dfrac{y+b.\sqrt{y}}{b.\sqrt{y}}$.
\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{5}{2\sqrt{5}}=\frac{10\sqrt{5}}{20}=\frac{\sqrt{5}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{3\sqrt{20}}{180}=\frac{\sqrt{20}}{60}=\frac{2\sqrt{5}}{60}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{10\sqrt{2}\left(\sqrt{2}+1\right)}{50}=\frac{20+10\sqrt{2}}{50}=\frac{10\left(2+\sqrt{2}\right)}{50}=\frac{2+\sqrt{2}}{5}\)
\(\frac{y+b\sqrt{y}}{b\sqrt{y}}=\frac{y\left(\sqrt{y}+b\right)}{by}=\frac{\sqrt{y}+b}{b}\)
510=5.1010.10=510(10)2=51010" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
5.105.2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
525=5.525.5=552.(5.5)=552(5)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
552.5=52" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
1320=1.20320.20=203.(20.20)=203.(20)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
203.20=22.560=2560=252.30=530" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
(22+2)5.2=(22+2).252.2=22.2+2.25.(2)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
2.2+225.2=2(2+2)5.2=2+25" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
y+byby=(y+by).yby.y=yy+by.yb.(y)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
yy+b(y)2by=yy+byby" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
y(y+b)b.y=y+bb" role="presentation" style="border:0px; direction:ltr; display:inline-table; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">.
y+byby=(y)2+byby" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
Nguồn : Bài 50 trang 30 SGK Toán 9 tập 1 - loigiaihay.com
#Ye Chi-Lien
\(\dfrac{5}{\sqrt{10}}=\dfrac{\sqrt{10}}{2}\)
\(\dfrac{5}{2\cdot\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)
\(\dfrac{1}{3\cdot\sqrt{20}}=\dfrac{\sqrt{20}}{60}\) ;
Xem thêm câu trả lời
Tính:
\(\left(\dfrac{3\sqrt{3}-2\sqrt{2}}{\sqrt{3}-\sqrt{2}}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}\right)\cdot\dfrac{5-2\sqrt{6}}{4}\)
Ta có: \(\left(\dfrac{3\sqrt{3}-2\sqrt{2}}{\sqrt{3}-\sqrt{2}}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}\right)\cdot\dfrac{5-2\sqrt{6}}{4}\)
\(=\left(\dfrac{\left(\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{6}+2\right)}{\sqrt{3}-\sqrt{2}}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\right)\cdot\dfrac{5-2\sqrt{6}}{4}\)
\(=\left(5+\sqrt{6}+\sqrt{6}\right)\cdot\dfrac{5-2\sqrt{6}}{4}\)
\(=\dfrac{\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)}{4}\)
\(=\dfrac{25-24}{4}=\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
Bài 72 (trang 40 SGK Toán 9 Tập 1)
Phân tích thành nhân tử (với các số $x, y, a, b$ không âm và $a \geq b$)
a) $x y-y \sqrt{x}+\sqrt{x}-1$ ; b) $\sqrt{a x}-\sqrt{b y}+\sqrt{b x}-\sqrt{a y}$ ;
c) $\sqrt{a+b}+\sqrt{a^{2}-b^{2}}$ ; d) $12-\sqrt{x}-x$
\(a,\left(\sqrt{8}-3.\sqrt{2}+\sqrt{10}\right)\sqrt{2}-\sqrt{5}\)
\(=\sqrt{8}.\sqrt{2}-3\sqrt{2}.\sqrt{2}+\sqrt{10}.\sqrt{2}-\sqrt{5}\)
\(=\sqrt{16}-3.2+\sqrt{20}-\sqrt{5}\)
\(=\sqrt{4^2}-6+\sqrt{2^2.5}-\sqrt{5}\)
\(=2-6+2\sqrt{5}-\sqrt{5}\)
\(=-2+\sqrt{5}\)
\(b,\)
\(0,2\sqrt{\left(-10^2\right).3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\)
\(=0,2.\left|-10\right|.\sqrt{3}+2\left|\sqrt{3}-\sqrt{5}\right|\)
\(=0,2.10.\sqrt{3}+2\left(\sqrt{5}-\sqrt{3}\right)\)
\(=2\sqrt{3}+2\sqrt{5}-2\sqrt{3}\)
\(=2\sqrt{5}\)
a)
x
y
−
y
√
x
+
√
x
−
1
=
y
⋅
√
x
⋅
√
x
−
y
√
x
+
√
x
−
1
=
y
√
x
(
√
x
−
1
)
+
(
√
x
−
1
)
=
(
√
x
−
1
)
(
y
√
x
+
1
)
.
b)
√
a
x
−
√
b
y
+
√
b
x
−
√
a
y
=
(
√
a
x
+
√
b
x
)
−
(
√
a
y
+
√
b
y
)
=
(
√
a
⋅
√
x
+
√
b
⋅
√
x
)
−
(
√
a
⋅
√
y
+
√
b
⋅
√
y
)
=
√
x
(
√
a
+
√
b
)
−
√
y
(
√
a
+
√
b
)
=
(
√
a
+
√
b
)
(
√
x
−
√
y
)
.
c)
√
a
+
b
+
√
a
2
−
b
2
=
√
a
+
b
+
√
(
a
+
b
)
(
a
−
b
)
=
√
a
+
b
+
√
a
+
b
⋅
√
a
−
b
=
√
a
+
b
(
1
+
√
a
−
b
)
.
d)
12
−
√
x
−
x
=
12
−
4
√
x
+
3
√
x
−
x
=
4
(
3
−
√
x
)
+
√
x
(
3
−
√
x
)
=
(
3
−
√
x
)
(
4
+
√
x
Xem thêm câu trả lời
1.\(\dfrac{\sqrt{8-4\sqrt{3}}}{\sqrt{\sqrt{6}-\sqrt{2}}}\cdot\sqrt{\sqrt{6}+\sqrt{2}}\)
2.\(\sqrt{16-5\sqrt{7}}\left(5\sqrt{2}+\sqrt{14}\right)+\dfrac{6}{3+\sqrt{10}}\)
Câu 1:
Có: \(8-4\sqrt{3}=8-2\sqrt{12}=6+2-2\sqrt{6.2}=(\sqrt{6}-\sqrt{2})^2\)
\(\Rightarrow \sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}\)
Do đó:
\(\frac{\sqrt{8-4\sqrt{3}}}{\sqrt{\sqrt{6}-\sqrt{2}}}.\sqrt{\sqrt{6}+\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{\sqrt{\sqrt{6}-\sqrt{2}}}.\sqrt{\sqrt{6}+\sqrt{2}}=\sqrt{\sqrt{6}-\sqrt{2}}.\sqrt{\sqrt{6}+\sqrt{2}}\)
\(=\sqrt{(\sqrt{6})^2-(\sqrt{2})^2}=\sqrt{6-2}=2\)
Đúng 0
Bình luận (0)
Câu 2:
\(16-5\sqrt{7}=\frac{32-10\sqrt{7}}{2}=\frac{32-2\sqrt{175}}{2}=\frac{25+7-2\sqrt{25.7}}{2}=\frac{(5-\sqrt{7})^2}{2}\)
\(\Rightarrow \sqrt{16-5\sqrt{7}}=\frac{5-\sqrt{7}}{\sqrt{2}}\)
Do đó:
\(\sqrt{16-5\sqrt{7}}(5\sqrt{2}+\sqrt{14})+\frac{6}{3+\sqrt{10}}=\frac{5-\sqrt{7}}{\sqrt{2}}.\sqrt{2}(5+\sqrt{7})+\frac{6(3-\sqrt{10})}{(3+\sqrt{10})(3-\sqrt{10})}\)
\(=(5-\sqrt{7})(5+\sqrt{7})+\frac{18-6\sqrt{10}}{3^2-10}=25-7+(-18+6\sqrt{10})\)
\(=6\sqrt{10}\)
Đúng 0
Bình luận (0)
pdfrac{2}{1-sqrt{2}}-dfrac{2}{1+sqrt{2}}
Qleft(dfrac{sqrt{6}-sqrt{2}}{1-sqrt{3}}-dfrac{5}{sqrt{5}}right)cdotleft(sqrt{5}-sqrt{2}right)
Rdfrac{2}{7+4sqrt{3}}+dfrac{2}{7-4sqrt{3}}
Sdfrac{2}{sqrt{5}+1}-sqrt{dfrac{2}{3-sqrt{5}}}
Tdfrac{4}{1-sqrt{3}}-dfrac{sqrt{15}+sqrt{3}}{1+sqrt{5}}
Uleft(dfrac{1}{2-sqrt{5}}+dfrac{2}{sqrt{5}+sqrt{3}}right):dfrac{1}{sqrt{21-12sqrt{3}}}
Vdfrac{2}{sqrt{3}-1}-sqrt{dfrac{2}{6-3sqrt{3}}}
Wdfrac{5sqrt{3}}{sqrt{3-sqrt{5}}-sqrt{3}}-dfrac{5sqrt{3}}{sqrt{3-sqrt{5}}+sqr...
Đọc tiếp
\(p=\dfrac{2}{1-\sqrt{2}}-\dfrac{2}{1+\sqrt{2}}\)
\(Q=\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right)\cdot\left(\sqrt{5}-\sqrt{2}\right)\)
\(R=\dfrac{2}{7+4\sqrt{3}}+\dfrac{2}{7-4\sqrt{3}}\)
\(S=\dfrac{2}{\sqrt{5}+1}-\sqrt{\dfrac{2}{3-\sqrt{5}}}\)
\(T=\dfrac{4}{1-\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\)
\(U=\left(\dfrac{1}{2-\sqrt{5}}+\dfrac{2}{\sqrt{5}+\sqrt{3}}\right):\dfrac{1}{\sqrt{21-12\sqrt{3}}}\)
\(V=\dfrac{2}{\sqrt{3}-1}-\sqrt{\dfrac{2}{6-3\sqrt{3}}}\)
\(W=\dfrac{5\sqrt{3}}{\sqrt{3-\sqrt{5}}-\sqrt{3}}-\dfrac{5\sqrt{3}}{\sqrt{3-\sqrt{5}}+\sqrt{3}}\)
\(Y=\dfrac{\sqrt{2}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}\)
♡
\(\dfrac{2}{1-\sqrt{2}}-\dfrac{2}{1+\sqrt{2}}\)
\(=\dfrac{2\left(1+\sqrt{2}\right)-2\left(1-\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}\)
\(=\dfrac{2+2\sqrt{2}-2+2\sqrt{2}}{1-2}=-4\sqrt{2}\)
♡\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left[-\dfrac{\sqrt{2}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}-\sqrt{5}\right]\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-3\)
♡\(\dfrac{2}{7+4\sqrt{3}}+\dfrac{2}{7-4\sqrt{3}}\)
\(=\dfrac{2\left(7-4\sqrt{3}\right)+2\left(7+4\sqrt{3}\right)}{\left(7+4\sqrt{3}\right)\left(7-4\sqrt{3}\right)}\)
\(=\dfrac{14-8\sqrt{3}+14+8\sqrt{3}}{49-48}\)
= 28
Đúng 0
Bình luận (0)
♡
\(\dfrac{2}{\sqrt{5}+1}-\sqrt{\dfrac{2}{3-\sqrt{5}}}\)
\(=\dfrac{2}{\sqrt{5}+1}-\sqrt{\dfrac{4}{6-2\sqrt{5}}}\)
\(=\dfrac{2}{\sqrt{5}+1}-\dfrac{2}{\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{2\left(\sqrt{5}-1\right)-2\left(\sqrt{5}+1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{2\sqrt{5}-2-2\sqrt{5}-2}{5-1}\)
= - 1
♡\(\dfrac{4}{1-\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\)
\(=\dfrac{4\left(1+\sqrt{3}\right)}{1-3}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{\left(\sqrt{5}+1\right)}\)
\(=-2-2\sqrt{3}-\sqrt{3}=-2-3\sqrt{3}\)
♡\(\dfrac{\sqrt{2}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}\)
\(=\dfrac{2}{4+\sqrt{6+2\sqrt{5}}}\) (nhân [căn 2] vào cả tử và mẫu)
\(=\dfrac{2}{4+\sqrt{\left(\sqrt{5}+1\right)^2}}\)
\(=\dfrac{2}{5+\sqrt{5}}=\dfrac{2\left(5-\sqrt{5}\right)}{25-5}=\dfrac{5-\sqrt{5}}{10}\)
Đúng 0
Bình luận (0)
Bài 71 (trang 40 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $(sqrt{8}-3 . sqrt{2}+sqrt{10}) sqrt{2}-sqrt{5}$ ; b) $0,2 sqrt{(-10)^{2} cdot 3}+2 sqrt{(sqrt{3}-sqrt{5})^{2}}$ ;
c) $left(dfrac{1}{2} cdot sqrt{dfrac{1}{2}}-dfrac{3}{2} cdot sqrt{2}+dfrac{4}{5} cdot sqrt{200}right): dfrac{1}{8}$ ; d) $2 sqrt{(sqrt{2}-3)^{2}}+sqrt{2 cdot(-3)^{2}}-5 sqrt{(-1)^{4}}$
Đọc tiếp
Bài 71 (trang 40 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $(\sqrt{8}-3 . \sqrt{2}+\sqrt{10}) \sqrt{2}-\sqrt{5}$ ; b) $0,2 \sqrt{(-10)^{2} \cdot 3}+2 \sqrt{(\sqrt{3}-\sqrt{5})^{2}}$ ;
c) $\left(\dfrac{1}{2} \cdot \sqrt{\dfrac{1}{2}}-\dfrac{3}{2} \cdot \sqrt{2}+\dfrac{4}{5} \cdot \sqrt{200}\right): \dfrac{1}{8}$ ; d) $2 \sqrt{(\sqrt{2}-3)^{2}}+\sqrt{2 \cdot(-3)^{2}}-5 \sqrt{(-1)^{4}}$
a) (√8 - 3√2 + √10)√2 - √5
= (√22.2 - 3√2 + √5.2)√2 - √5
= (2√2 - 3√2 + √5.√2)√2 - √5
= (2 - 3 + √5)√2.√2 - √5
= (-1 + √5).2 - √5
= -2 + 2√5 - √5
= -2 + √5
b) 0,2√((-10)2.3) + 2√(√3 - √52)
= 0,2.10√3 + 2|√3 - √5|
= 2√3 + 2(√5 - √3)
= 0,2.10.√3 + 2|√3 - √5|
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3
= 2√5
Giải phần c và d
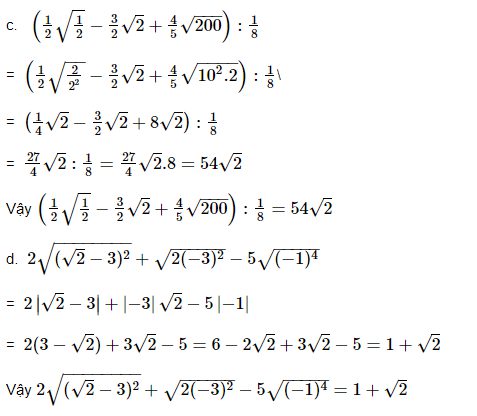
a) -2 + \(\sqrt{5}\)
b) 2\(\sqrt{5}\)
c) 54\(\sqrt{2}\)
d) 1 + \(\sqrt{2}\)
Xem thêm câu trả lời


