1
cho hàm số y=f (x)=-2x chứng minh hàm số nghịch biến trên tập số thực R
Cho hàm số y = f(x) = 4 - 2/5x với x ∈ R. Chứng minh rằng hàm số đã cho nghịch biến trên R.
Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.
cho hàm số y=f(x)=1/3x.Chứng minh hàm số đã cho đồng biến trên tập hợp số thực R
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Cho hàm số y=-5/9x-6
a) Tính f(-1),f(0),f(2),f(1/2)
b)Chứng minh hàm số luôn nghịch biến trên R
b: Vì \(a=-\dfrac{5}{9}< 0\) nên hàm số luôn nghịch biến trên R
Cho hàm số y=-2x + 5. Chứng minh rằng hàm số nghịch biến trên R
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị hàm số y = f ' ( x ) như hình bên:
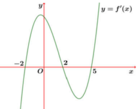
Hỏi hàm số g ( x ) = f ( 3 - 2 x ) nghịch biến trên khoảng nào sau đây?
A. (-1;+∞)
B. (-∞;-1)
C. (1;3)
D. (0;2)
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng

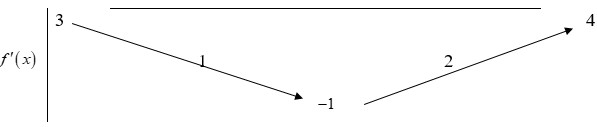
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
Cho hàm số y=(-m2+m-4)x+3 (m là tham số). Hàm số đã cho đồng biến hay nghịch biến trên tập hợp số thực R? Vì sao?
\(\text{Ta có:}-m^2+m-4\\ =-\left(m^2-m+4\right)\\ =-\left[\left(m^2-m+\dfrac{1}{4}\right)+\dfrac{15}{4}\right]\\ =-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}\le-\dfrac{15}{4}< 0\)
Vậy HSNB trên R
\(-m^2+m-4\)
\(=-\left(m^2-m+4\right)\)
\(=-\left(m^2-m+\dfrac{1}{4}+\dfrac{15}{4}\right)\)
\(=-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}< 0\forall m\)
Vậy: Hàm số nghịch biến trên R
chứng minh rằng hàm số y=f(x)= -x+1 nghịch biến trên R. so sánh f(1- căn 2) và f(1+ căn 2)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-x_1+1+x_2-1}{x_1-x_2}=-1\)
Vậy: f(x) nghịch biến trên R