Hình thang ABCD có đáy AB,CD
Cho biết AB=CD. Chứng minh rằng AD//BC,AD=BC. Giúp mình vs
Hình thang ABCD có đáy AB, CD.
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
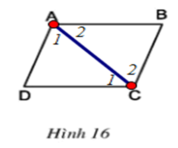
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
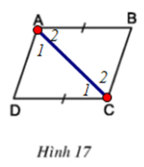
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
hình thang ABCD có đáy AB,CD
a) Cho biết AD//BC. Chứng minh AD=BC, AB=CD
b) Cho biết AB=Cd. Chứng minh AD//BC, AC=BC
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC
Hình thang ABCD có đáy AB,CD
a)Cho biết AD//BC.Chứng minh AD=BC,AB=CD
b)Cho biết AB=CD.Chứng minh rằng AD//BC,AD=BC
a) Ta có : AB // CD ( do ABCD là hình thang )
AD // BC ( gt )
=> ABCD là hình bình hành
=> AD = BC ; AB = CD
b) Ta có : AB = CD ( gt )
AB // CD ( gt )
=> ABCD là hình bình hành
=> AD // BC ; AD = BC
Cho hình thang cân ABCD (AB//CD, AB<CD) có AB=AD. chứng minh rằng DC-AB<AD+BC
Qua P kẻ đường thẳng song song với AD cắt CD tại P. Khi đó dễ thấy \(AB=DP\). Từ đó \(DC-AB=DC-DM=CM\)
Mặt khác, \(AD=BM\) nên \(AD+BC=BM+BC\).
Hiển nhiên \(CM< BM+BC\). Điều này dẫn đến \(DC-AB< AD+BC\) (đpcm)
Cho hình thang ABCD có đáy AB < đáy CD. Chứng minh rằng nếu góc ADC = góc BCD thì AD = BC.
- Hình bạn tự vẽ nhé!
- Kéo dài AD và BC cắt nhau tại E
- Vì ABCD là hình thang
=> AB // DC
=> góc EAB = góc EDC
góc EBA = góc ECD
( các góc đồng vị)
mà góc EDC = góc ECD (gt)
=> góc EAB = góc EBA (bắc cầu)
=> tam giác EAB cân tại E
tam giác EDC cân tại E
=> EA = EB
ED = EC
=> ED - EA = EC - EB (bắc cầu)
=> AD = BC (đpcm)
Chúc bạn học tốt <3
Xét hình thang ABCD có \(\widehat{ADC}=\widehat{BCD}\)
nên ABCD là hình thang cân
Suy ra: AD=BC
Bài 1. Cho hình thang cân ABCD (AB\\CD) có AB=8cm, BC=AD=5cm, CD=14cm. Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Chứng minh: CD-AB=2AK. Từ đó tính độ dài BH.
c) Tính diện tích hình thang ABCD.
Bài 2. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc BCD.
Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Bài 7. Cho hình thang ABCD, đáy AB = 40cm, CD = 80cm, BC = 50cm, AD = 30cm. Chứng minh rằng ABCD là hình thang vuông.
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2
=> 502= 30^2 +40^2
=> 50^2 = 2500
=> 50^2 = 50^2
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2AG2=AD2+DG2
⇒502=302+402⇒502=302+402
⇒502=900+1600
⇒502=2500
⇒502=502
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
hơi dài nha![]()
Cho hình thang cân ABCD có đáy lớn BC. Giả sử đường cao AH thỏa mãn AH^2= AD*BC. Gọi P là hình chiếu của H lên AB. Chứng minh rằng: AB=CD=1/2(AD+BC),AP=2AD*BC/(BC+AD)
Cho hình thang cân ABCD có đáy lớn BC. Giả sử đường cao AH thỏa mãn AH^2= AD*BC. Gọi P là hình chiếu của H lên AB. Chứng minh rằng: AB=CD=1/2(AD+BC),AP=2AD*BC/(BC+AD)
Hình thang ABCD có đáy AB,CD
a) Cho biết AD // BC. Chứng minh rằng AD = BC, AB = CD
b ) Cho biết AB = CD. Chứng minh rằng AD // với BC, AD = BC
* ?2 ( SGK/70 )
a) Kẻ đoạn thẳng AC.
Ta có: AB // CD (ABCD là hình thang)
Xét \(\Delta ABC\) và \(\Delta DCA\), có:
\(\widehat{BAC} = \widehat{ACD}\) (hai góc so le trong, AB//CD)
AC là cạnh chung
\(\widehat{DAC} = \widehat{BCA}\) (hai góc so le trong, AD // BC)
Vậy \(\Delta ABC=\Delta CDA\) (g.c.g)
\(\Rightarrow AD=BC;AB=CD\) (ĐPCM)
b) Xét \(\Delta ADC\) và \(\Delta CBA\), có:
AB = CD (gt)
\(\widehat{BAC} = \widehat{ACD}\) ((hai góc so le trong, AB//CD)
AC là cạnh chung
\(\Rightarrow\Delta ADC=\Delta CBA\) (c.g.c)
\(\Rightarrow\) \(\widehat{DAC} = \widehat{BCA}\) (hai góc tương ứng), mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AD // BC
Ta có: \(\Delta ADC=\Delta CBA\) \(\Rightarrow\) AD = BC (hai cạnh tương ứng)
Vậy AD // BC, AD = BC (đpcm)