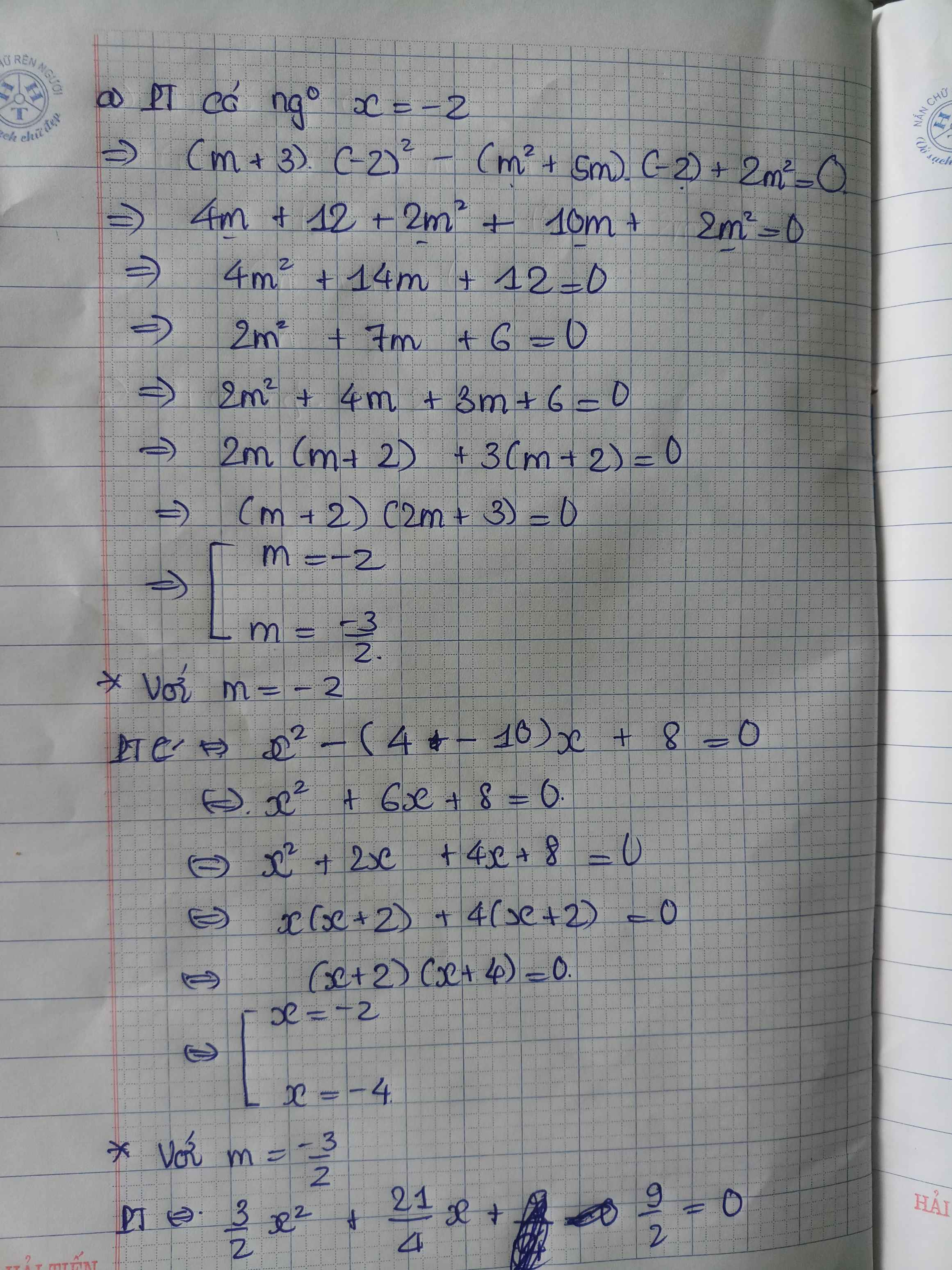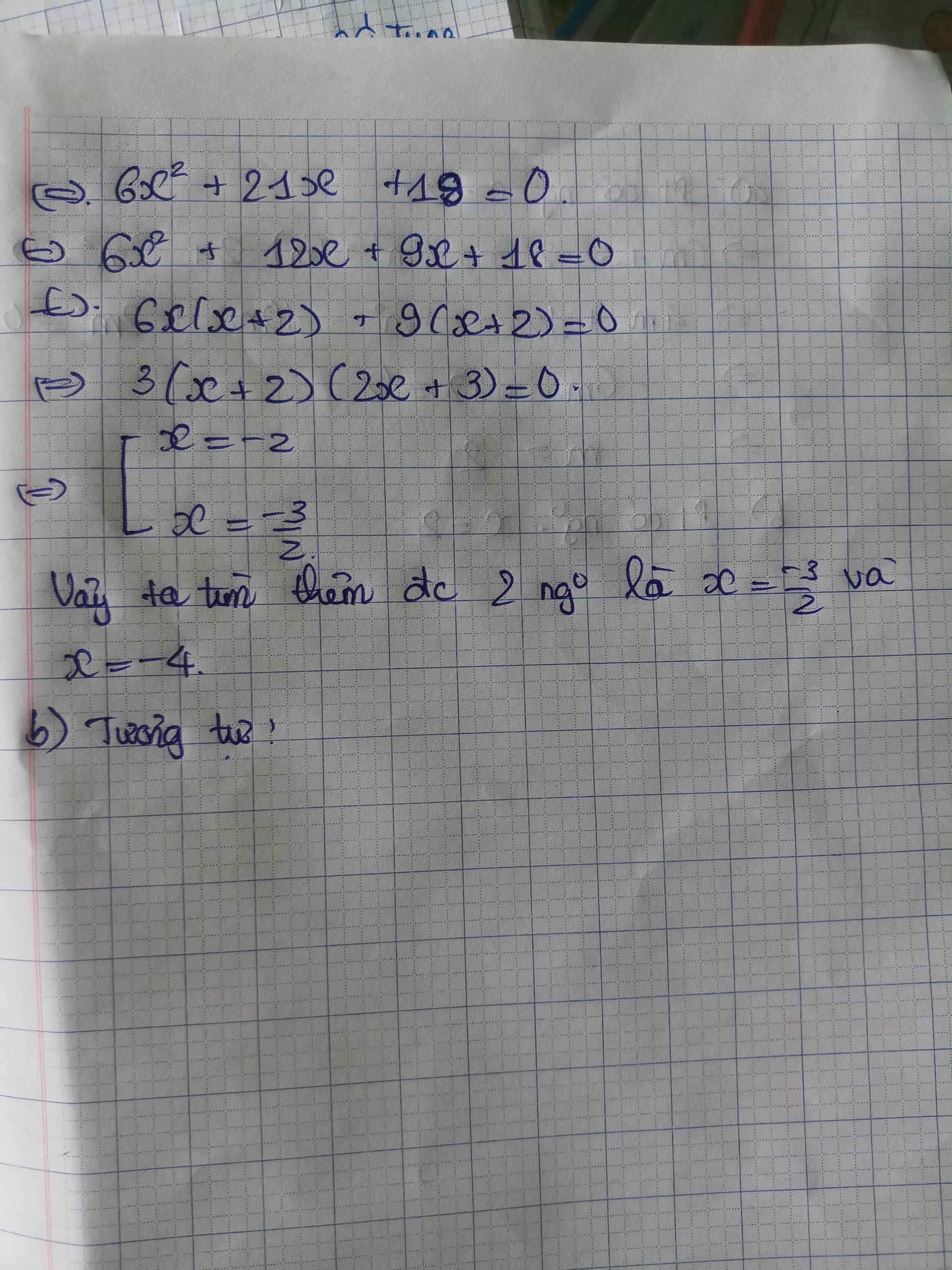Tìm m để 2 phương trình sau có nghiệm chung \(x^2-\left(2m-3\right)x+6=0\) và \(2x^2+x+m-5=0\)
H24
Những câu hỏi liên quan
Tìm m để 2 phương trình có nghiệm chung \(x^2-\left(2m-3\right)x+6=0\) và \(2x^2+x+m-5=0\)
Tìm m để hai phương trình sau có nghiệm chung
a \(2x^2+\left(3m-1\right)x-3=0\) và \(6x^2-\left(2m-1\right)x-1=0\)
b \(x^2-mx+2m+1=0\) và \(mx^2-\left(2m+1\right)x-1=0\)
câu a
Gọi x0 là nghiệm chung của PT(1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}2x^2_0+\left(3m-1\right)x_0-3=0\left(\times3\right)\\6.x^2_0-\left(2m-1\right)x_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x^2_0+3\left(3m-1\right)x_0-9=0\left(1\right)\\6x^2_0-\left(2m-1\right)x_0-1=0\left(2\right)\end{matrix}\right.\) Lấy (1)-(2) ,ta được
PT\(\Leftrightarrow3\left(3m-1\right)-9+\left(2m-1\right)+1\)=0
\(\Leftrightarrow9m-3-9+2m-1+1=0\Leftrightarrow11m-12=0\)
\(\Leftrightarrow m=\dfrac{12}{11}\)
Đúng 1
Bình luận (0)
tìm m để phương trình sau có nghiệm
\(\left(m-2\right)x^2+2\left(2m-3\right)x+5m-6=0\)
- Với \(m=2\) pt có nghiệm
- Với \(m\ne2\) để pt có nghiệm
\(\Rightarrow\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\)
\(\Leftrightarrow-m^2+4m-3\ge0\Rightarrow1\le m\le3\)
Vậy \(1\le m\le3\)
Đúng 0
Bình luận (0)
Tìm m để các phương trình sau (dùng công thức nghiệm thu gọn)
a.\(x^2+2\left(m-2\right)x+m^2-3=0\) có nghiệm
b.\(\left(2m-1\right)x-4mx+2m+3=0\) có nghiệm kép
c.\(4x^2-2\left(2m-1\right)x+m^2=0\) vô nghiệm
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4
Đúng 0
Bình luận (0)
Tìm m để 2 phương trính sau có nghiệm chung: x2-(2m-3).x+6=0 và 2x2+x+m-5=0
a) Tìm m để phương trình\(\left(m+3\right)x^2-\left(m^2+5m\right)x+2m^2=0\) có nghiệm x=-2
tìm nghiệm còn lại
b Tìm m để phương trình \(\left(m^2-1\right)x^2-2mx+m^2+m+4=0\) có nghiệm x=2
Tìm nghiệm còn
lại?
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm m để :
a. Phương trình \(x^2-\left(2m+1\right)x+m^2-3=0\) có nghiệm kép
b. Phương trình \(x^2-3mx+m-2=0\) vô nghiệm
c. Phương trình \(x^2-2\left(m-1\right)x+m^2=0\) có nghiệm
a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2
Đúng 1
Bình luận (0)
Bài 1: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm trái dấu:a,left(m^2-1right)x^2+left(m+3right)x+left(m^2+mright)0b,x^2-left(m^2+m-2right)x+m^2+m-50Bài 2: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm dương phân biệt:a,x^2-2x+m^2+m+30b,left(m^2+m+1right)x^2+left(2m-3right)x+m-50c,x^2-6mx+2-2m+9m^20
Đọc tiếp
Bài 1: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm trái dấu:
\(a,\left(m^2-1\right)x^2+\left(m+3\right)x+\left(m^2+m\right)=0\)
\(b,x^2-\left(m^2+m-2\right)x+m^2+m-5=0\)
Bài 2: Tìm các giá trị của tham số m để mỗi phương trình sau có 2 nghiệm dương phân biệt:
\(a,x^2-2x+m^2+m+3=0\)
\(b,\left(m^2+m+1\right)x^2+\left(2m-3\right)x+m-5=0\)
\(c,x^2-6mx+2-2m+9m^2=0\)
Tìm m để phương trình sau có nghiệm kép.Tìm nghiệm kép đó?
a. \(x^2+3x+m-2=0\)
b. \(x^2+3x-2m+1=0\)
c. \(x^2+2mx+m^2-2m-3=0\)
d. \(x^2+\left(2m-3\right)x+m^2=0\)
Bài 1: Tìm m để phương trình left(m-1right)x^2+2x+m0 có ít nhất một nghiệm không âmBài 2: Với giá trị nào của a,b các phương trình bậc hai sau có 2 nghiệm chungleft(2a+1right)x^2-left(3a-1right)x+20left(b+2right)x^2-left(2b+1right)x-10Bài 3: a) Với giá trị nào của m thì 2 phương trình sau có nghiệm chung2x^2+mx-10 và mx^2-x+20b) Tim min Z để 2 phương trình sau có ít nhất 1 nghiệm chungx^2-mx-20 và x^2-x+6m0Bài 5: left(m+1right)x^2-2left(m+2right)+m-30Tìm m để phương trình sau có 2 nghiệm x1,x2 t...
Đọc tiếp
Bài 1: Tìm m để phương trình \(\left(m-1\right)x^2+2x+m=0\) có ít nhất một nghiệm không âm
Bài 2: Với giá trị nào của a,b các phương trình bậc hai sau có 2 nghiệm chung
\(\left(2a+1\right)x^2-\left(3a-1\right)x+2=0\)
\(\left(b+2\right)x^2-\left(2b+1\right)x-1=0\)
Bài 3: a) Với giá trị nào của m thì 2 phương trình sau có nghiệm chung
\(2x^2+mx-1=0\) và \(mx^2-x+2=0\)
b) Tim \(m\in Z\) để 2 phương trình sau có ít nhất 1 nghiệm chung
\(x^2-mx-2=0\) và \(x^2-x+6m=0\)
Bài 5: \(\left(m+1\right)x^2-2\left(m+2\right)+m-3=0\)
Tìm m để phương trình sau có 2 nghiệm x1,x2 thỏa mãn:
a) \(x_1-3x_2=3\)
b) \(\left(4x_1+1\right)\left(4x_2+1\right)=18\)
Nhiều thế, chắc phải đưa ra đáp thôi
Đúng 0
Bình luận (0)