đố everybody
x4 - 2x3 +x2 +2x-2=0
Tìm Max và min của x khi x thuộc khoảng [1;3]
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm GTLN (max), GTNN (min) của y = x 2 - x + 2 x - 1 khi x ∈ 3 2 ; 3
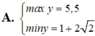
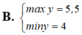
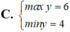
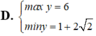
tìm x
a 5x3-7x2-15x+21=0
b (x-3)2=4x2-20x+25
c x+x2-x3-x4=0
d 2x3+3x2+2x+3=0
b: 4x^2-20x+25=(x-3)^2
=>(2x-5)^2=(x-3)^2
=>(2x-5)^2-(x-3)^2=0
=>(2x-5-x+3)(2x-5+x-3)=0
=>(3x-8)(x-2)=0
=>x=8/3 hoặc x=2
c: x+x^2-x^3-x^4=0
=>x(x+1)-x^3(x+1)=0
=>(x+1)(x-x^3)=0
=>(x^3-x)(x+1)=0
=>x(x-1)(x+1)^2=0
=>\(x\in\left\{0;1;-1\right\}\)
d: 2x^3+3x^2+2x+3=0
=>x^2(2x+3)+(2x+3)=0
=>(2x+3)(x^2+1)=0
=>2x+3=0
=>x=-3/2
a: =>x^2(5x-7)-3(5x-7)=0
=>(5x-7)(x^2-3)=0
=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)
phân tích thành nhân tử:
a, (ab-1)2 +( a+b)2 x3 + 2x2 + 2x + 1;
c, x3 - 4x2 + 12x - 27; x4 - 2x3 + 2x -1
d, x4 +2x3+ 2x2 +2x + 1 x2-2x-4y2-4y
e, x4 + 2x3 - 4x -4 x2(1 - x2) - 4 - 4x2
f, (1 + 2x) (1-2x) - x(x+2)(x-2) x2 + y2 - x2y2 + xy- x - y
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
Bài 4. Tính tổng và hiệu của các đa thức sau:
a) P(x) = 5x4 + 3x2 - 3x5 + 2x - x2 - 4 +2x5 và Q(x) = x5 - 4x4 + 7x - 2 + x2 - x3 + 3x4 - 2x2
b) H (x) = ( 3x5 - 2x3 + 8x + 9) - ( 3x5 - x4 + 1 - x2 + 7x) và R( x) = x4 + 7x3 - 4 - 4x ( x2 + 1) + 6x
ai giúp mình với
`@` `\text {Ans}`
`\downarrow`
`a)`
Thu gọn:
`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)
`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`
`= -x^5 + 5x^4 + 2x^2 + 2x - 4`
`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)
`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`
`= x^5 - x^4 - x^3 - x^2 + 7x - 2`
`@` Tổng:
`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`
`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`
`= 4x^4 - x^3 + x^2 + 9x - 6`
`@` Hiệu:
`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`
`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`
`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`
`b)`
`@` Thu gọn:
\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)
`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`
`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`
`= x^4 - 2x^3 - x^2 + 15x + 10`
\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)
`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`
`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`
`= x^4 + 3x^3 + 2x - 4`
`@` Tổng:
`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)
`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`
`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`
`= 2x^4 + x^3 - x^2 + 17x + 6`
`@` Hiệu:
`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)
`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`
`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`
`= -5x^3 - x^2 + 13x + 14`
`@` `\text {# Kaizuu lv u.}`
7) x4+2x3-2x2+2x-3=0
8) (x-1)( x2+5x-2)-x3+1=0
9) x2+(x+2)(11x-7)=4
(GIẢI PHƯƠNG TRÌNH)
\(x^4+2x^3-2x^2+2x-3=0\\ \Leftrightarrow x^4+3x^3-x^3-3x^2+x^2+3x-x-3=0\\ \Leftrightarrow x^3\left(x+3\right)-x^2\left(x+3\right)+x\left(x+3\right)-\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x^3-x^2+x-1\right)=0\\ \Leftrightarrow\left(x+3\right)\left[x^2\left(x-1\right)+\left(x-1\right)\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\\x^2+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\left(\text{vì }x^2+1\ge1>0\right)\)
Vậy ...
\(\left(x-1\right)\left(x^2+5x-2\right)-x^3+1=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+5x-2\right)-\left(x^3-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+5x-2\right)-\left(x-1\right)\left(x^2+x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left[\left(x^2+5x-2\right)-\left(x^2+x+1\right)\right]=0\\ \Leftrightarrow\left(x-1\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy ...
\(x^2+\left(x+2\right)\left(11x-7\right)=4\\ \Leftrightarrow x^2-4+\left(x+2\right)\left(11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x-2\right)+\left(11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x-2+11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(12x-9\right)=0\\ \Leftrightarrow3\left(x+2\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+2=0\\4x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy ...
(2−3xx2+2x−3−x+31−x−x+1x+3):3x+12x3−1(2−3xx2+2x−3−x+31−x−x+1x+3):3x+12x3−1
và B=x2+x−2x3−1x2+x−2x3−1
a Rút gọn biểu thức M=A.B
b Tìm x thuộc Z để M thuộc Z
c Tìm GTLN của biểu thức N=A−1−B
Bài 1 . cho hai đa thức: P(x) = 4x4 - 2x3 - 7x2 + 2x + 1/3 và Q(x) = x4 + 3x3 - 6x2 - x - 1/4
a. Tính P(x) + Q(x);
b. Tính P(x) - Q(x).
Bài 2. cho đa thức: M(x) = x2 - 2x3 + x + 5 và N(x) = 2x3 - x - 6
a. Tính M(2)
b. Tìm đa thức A(x) sao cho A(x) = M(x) + N(x); A(x), tính B(x) = M(x) - N(x)
c. Tìm nghiệm của đa thức A(x)
Bài 3. Tìm nghiệm của các đa thức sau:
a. 2x - 8 b. 2x + 7 c. 4 - x2 d. 4x2 - 9
e. 2x2 - 6 f. x(x - 1) g. x + 2x h. x( x + 2 )
Bài 4. cho hai đa thức: f(x) = 2x4 + 3x2 - x + 1 - x2 - x4 - 6x3
g(x) = 10x3 + 3 - x4 - 4x3 + 4x - 2x2
a. Thu gọn đa thức: f(x), g(x) và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b. Tính h(x) = f(x) + g(x); K(x) = f(x) - g(x)
c. Tìm nghiệm của đa thức h(x)
Bài 5. Tìm nghiệm của các đa thức:
a. 9 - 3x b. -3x + 4 c. x2 - 9 d. 9x2 - 4
e. x2 - 2 f. x( x - 2 ) g. x2 - 2x h. x(x2 + 1 )
Tách ra, dài quá mn đọc là mất hứng làm đó.
x4 – 2x3 + 2x – 1
a3 – a4 + 2a3 + 2a2
x4 + x3 + 2x2 + x + 1
x4 + 2x3 + 2x2 + 2x + 1
x2y + xy2 + x2z + y2z + 2xyz
x3 + x4 + x3 + x2 + x + 1
a: Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x-1\right)^3\cdot\left(x+1\right)\)
b: Ta có: \(-a^4+a^3+2a^3+2a^2\)
\(=-a^2\left(a^2-a-2a-2\right)\)
c: Ta có: \(x^4+x^3+2x^2+x+1\)
\(=x^4+x^3+x^2+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^2+1\right)\)