10cos2x-5sinxcosx+3sin2x=4
AA
Những câu hỏi liên quan
cos2x-√3 sin2x=1+sin2x
10cos2x-5sinxcosx+3sin2x=4
Mọi người giải chi tiết giúp em với ạ em cảm ơn
1.
\(cos^2x-\sqrt{3}sin2x=1+sin^2x\)
\(\Leftrightarrow cos2x-\sqrt{3}sin2x=1\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow2x+\dfrac{\pi}{3}=\pm\dfrac{\pi}{3}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
2.
\(10cos^2x-5sinx.cosx+3sin^2x=4\)
\(\Leftrightarrow20cos^2x-10sinx.cosx+6sin^2x=8\)
\(\Leftrightarrow20cos^2x-10-10sinx.cosx+6sin^2x-3=-5\)
\(\Leftrightarrow7cos2x-5sin2x=-5\)
\(\Leftrightarrow\sqrt{74}\left(\dfrac{7}{\sqrt{74}}cos2x-\dfrac{5}{\sqrt{74}}sin2x\right)=-5\)
\(\Leftrightarrow cos\left(2x+arccos\dfrac{7}{\sqrt{74}}\right)=-\dfrac{5}{\sqrt{74}}\)
\(\Leftrightarrow2x+arccos\dfrac{7}{\sqrt{74}}=\pm arccos\dfrac{5}{\sqrt{74}}+k2\pi\)
\(\Leftrightarrow x=-\dfrac{1}{2}arccos\dfrac{7}{\sqrt{74}}\pm\dfrac{1}{2}arccos\dfrac{5}{\sqrt{74}}+k\pi\)
Đúng 2
Bình luận (0)
Tìm họ nguyên hàm
I
∫
9
cos
x
−
5
sin
x
cos
x
+
s
inx
d
x
.
A.
I
2
x
+
7
ln
cos...
Đọc tiếp
Tìm họ nguyên hàm I = ∫ 9 cos x − 5 sin x cos x + s inx d x .
A. I = 2 x + 7 ln cos x + s inx + C
B. I = 7 x + 2 ln cos x + s inx + C
C. I = 3 x 2 + 11 ln cos x + s inx 2 + C
D. I = 11 x 2 + 3 ln cos x + s inx 2 + C
Đáp án A
Ta viết 9 cos x − 5 sin x dưới dạng:
9 cos x − 5 sin x = a cos x + s inx + b cos x − s inx ⇒ a + b = 9 a − b = − 5 ⇒ a = 2 b = 7
Sở dĩ ta viết như vậy vì cos x + s inx ' = cos x − s inx
Ta có: I = ∫ d cos x + s inx cos x + s inx ⇔ I = 2 x + 7 ln cos x + s inx + C
Đúng 0
Bình luận (0)
Phương trình
2
sin
2
x
-5sinxcosx-
cos
2
x
-2 tương đương với:
Đọc tiếp
Phương trình 2 sin 2 x -5sinxcosx- cos 2 x = -2 tương đương với:
![]()
![]()
![]()
![]()
Đáp án A
Cách 1. Do các đáp án chứa 2x nên ta biến đổi theo cách hạ bậc.
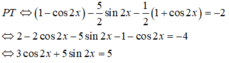
Cách 2. Nhập CASIO: ![]()
![]()
![]() là hệ số của đáp án, kết quả nào bằng 0 thì chọn
là hệ số của đáp án, kết quả nào bằng 0 thì chọn
Đúng 0
Bình luận (0)
Phương trình 2 sin 2 x - 5 sin x cos x - c o s 2 x = - 2 tương đương với
A. 3cos2x+5sin2x=5
B. 3cos2x+5sin2x=-5
C. 3cos2x-5sin2x=5
D. 3cos2x-5sin2x=-5
Phương trình
2
sin
2
x
-
5
sin
x
cos
x
-
cos
2
x
-2 tương đương với: A. 3cos2x + 5sin2x 5 B. 3cos2x + 5sin2x -5 C. 3cos2x - 5sin2x 5 D. 3cos2x - 5sin2x -5
Đọc tiếp
Phương trình 2 sin 2 x - 5 sin x cos x - cos 2 x = -2 tương đương với:
A. 3cos2x + 5sin2x = 5
B. 3cos2x + 5sin2x = -5
C. 3cos2x - 5sin2x= 5
D. 3cos2x - 5sin2x = -5
Đáp án A
Cách 1. Do các đáp án chứa 2x nên ta biến đổi theo cách hạ bậc.
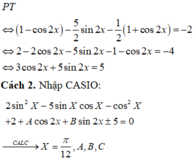
là hệ số của đáp án, kết quả nào bằng 0 thì chọn.
Đúng 0
Bình luận (0)
4(sin^3x+cos^3x)-3sin2x-4(cosx+sinx)=0
\(\Leftrightarrow4\left(sin^3x+cos^3x\right)-6sinx.cosx-4\left(sinx+cosx\right)=0\)
\(\Leftrightarrow4\left(sinx+cosx\right)^3-12sinx.cosx\left(sinx+cosx\right)-6sinx.cosx-4\left(sinx+cosx\right)=0\)
Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
Pt trở thành:
\(4t^3-6t\left(t^2-1\right)-3\left(t^2-1\right)-4t=0\)
\(\Leftrightarrow-2t^3-3t^2+2t+3=0\)
\(\Leftrightarrow\left(t^2-1\right)\left(2t+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t^2=1\\t=-\frac{3}{2}\left(l\right)\\\end{matrix}\right.\) \(\Rightarrow\left(sinx+cosx\right)^2=1\)
\(\Leftrightarrow2sinx.cosx=0\Leftrightarrow sin2x=0\)
\(\Rightarrow x=\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
Giải phương trình sau: 2cos2x - 3√3sin2x - 4sin2x = -4
Phương trình
2
sin
2
x
–
5
sin
x
cos
x
–
cos
2
x
+
2
0
có cùng tập nghiệm với phương trình nào trong số bốn phương trình sau: A.
4
sin
2
x
–
5
sin
x
cos
x
...
Đọc tiếp
Phương trình 2 sin 2 x – 5 sin x cos x – cos 2 x + 2 = 0 có cùng tập nghiệm với phương trình nào trong số bốn phương trình sau:
A. 4 sin 2 x – 5 sin x cos x - cos 2 x = 0
B. 4 sin 2 x + 5 sin x cos x + cos 2 x = 0
C. 4 tan 2 x – 5 tan x + 1 = 0
D. 5 sin 2 x + 3 cos 2 x = 2
Chọn C
Ta có:
2 sin 2 x − 5 sin x . c osx -cos 2 x + 2 = 0 ⇔ 2 sin 2 x − 5 sin x . c osx -cos 2 x + 2 ( sin 2 x + c os 2 x ) = 0 ⇔ 4 sin 2 x − 5 sin x . c osx + cos 2 x = 0 ( * )
* Lại có, cos x =0 không là nghiệm của phương trình trên .
Chia cả hai vế cho cos 2 x ta được: 4 tan 2 x - 5 tan x + 1 = 0
Nên đáp án chọn là C
Đúng 0
Bình luận (0)
Giải phương trình: (2cosx-1)(3sin2x-6cos2x+2cosx+4-\(3\sqrt{2}\) )+4sin2x=3





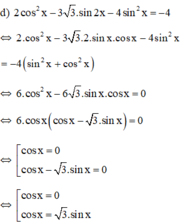
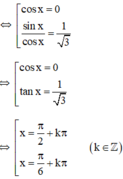
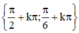 (k ∈ Z)
(k ∈ Z)

