Giải bất phương trình:
\(\dfrac{x-3}{2x+1}>0\)
giải các bất phương trình sau:
1) \(\dfrac{x^2-2x+5}{x-2}-x+1\ge0\) 2) \(\dfrac{2x-3}{x+1}-2< 0\)
1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
giải các bất phương trình tích và các bất phương trình thương
b/ \(\dfrac{3x+5}{2x^2-5x+3}\)≥0
c/2x3+x+3>0
Lời giải:
b/
\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)
c/
$2x^3+x+3>0$
$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$
$\Leftrightarrow (x+1)(2x^2-2x+3)>0$
$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$
$\Leftrightarrow x+1>0$
$\Leftrightarrow x>-1$
Bài 1. Giải các bất phương trình sau 1) \(\dfrac{2x-1}{x+1}-2< 0\) 2) \(\dfrac{x^2-2x+5}{x-2}-x+1\ge0\)
3) \(\dfrac{\left(1+2x\right)\left(x-3\right)}{\left(2x+3\right)\left(1-x\right)}\le0\) 4) \(\left|2x-3\right|>5\) 5)\(\left|1-2x\right|\le4\)
6) \(\left|3x+1\right|>x-2\)
\(\dfrac{2x-1}{x+1}-2< 0.\left(x\ne-1\right).\\ \Leftrightarrow\dfrac{2x-1-2x-2}{x+1}< 0.\Leftrightarrow\dfrac{-3}{x+1}< 0.\)
Mà \(-3< 0.\)
\(\Rightarrow x+1>0.\Leftrightarrow x>-1\left(TMĐK\right).\)
\(\dfrac{x^2-2x+5}{x-2}-x+1\ge0.\left(x\ne2\right).\\ \Leftrightarrow\dfrac{x^2-2x+5-x^2+2x+x-2}{x-2}\ge0.\\ \Leftrightarrow\dfrac{x+3}{x-2}\ge0.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3\ge0.\\x-2\ge0.\end{matrix}\right.\\\left\{{}\begin{matrix}x+3\le0.\\x-2\le0.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-3.\\x\ge2.\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-3.\\x\le2.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge2.\\x\le-3.\end{matrix}\right.\)
Kết hợp ĐKXĐ.
\(\Rightarrow\left[{}\begin{matrix}x>2.\\x\le-3.\end{matrix}\right.\)
\(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}\le0.\left(x\ne1;x\ne\dfrac{-3}{2}\right).\)
Đặt \(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}=f\left(x\right).\)
Ta có bảng sau:
| \(x\) | \(-\infty\) \(-\dfrac{3}{2}\) \(-\dfrac{1}{2}\) \(1\) \(2\) \(+\infty\) |
| \(1+2x\) | - | - 0 + | + | + |
| \(x-2\) | - | - | - | - 0 + |
| \(2x+3\) | - 0 + | + | + | + |
| \(1-x\) | + | + | + 0 - | - |
| \(f\left(x\right)\) | - || + 0 - || + 0 - |
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left(\dfrac{-3}{2};\dfrac{-1}{2}\right)\cup\)(1;2].
Giải các bất phương trình sau:
a)\(\dfrac{\left(2x-5\right)\left(x+2\right)}{-4x+3}>0\) b)\(\dfrac{x-3}{x+1}=\dfrac{x+5}{x-2}\)
a, \(\dfrac{\left(2x-5\right)\left(x+2\right)}{4x-3}< 0\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}\left(2x-5\right)\left(x+2\right)< 0\\4x-3>0\end{matrix}\right.\\\left\{{}\begin{matrix}\left(2x-5\right)\left(x+2\right)>0\\4x-3< 0\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-2< x< \dfrac{5}{2}\\x>\dfrac{3}{4}\end{matrix}\right.\\\left\{{}\begin{matrix}\left[{}\begin{matrix}x< -2\\x>\dfrac{5}{2}\end{matrix}\right.\\x< \dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\dfrac{3}{4}< x< \dfrac{5}{2}\\x< -2\end{matrix}\right.\)
Vậy tập nghiệm của bất phương trình là
S = \(\left(\dfrac{3}{4};\dfrac{5}{2}\right)\cup\left(-\infty;-2\right)\)
b, Pt
⇔ \(\left\{{}\begin{matrix}x^2-5x+6=x^2+6x+5\\x\in R\backslash\left\{-1;2\right\}\end{matrix}\right.\)
⇔ x = \(\dfrac{1}{11}\)
Vậy S = \(\left\{\dfrac{1}{11}\right\}\)
Giải bất phương trình
x2-2x+1<9
(x-1)(4-x2)≥0
\(\dfrac{x+2}{x-5}\)<0
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
câu 1 giải các phương trình sau.
a) 4x+8=3x-15
b) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)
câu 2 giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x-8\(\ge\)0.
b)10+10x>0
câu 3 giải bài toán bằng các lập phương trình
Một học sinh đi từ nhà đến trường với vận tốc 15km/h,rồi từ trường về nhà với vận tốc 20km/h.Biết thời gian đi nhiều hơn thời gian về là 15 phút. Tĩnh quãng đường từ nhà đến trường của người đó.
câu 4 Cho hình chữ nhật ABCD có AB=8cm,BC=6cm.Kẻ đường cao AH của tam giác ADB(AH\(\perp\)DB,H\(\in\)DB).
a) Chúng minh \(\Delta\)HAD đồng dạng \(\Delta\)ABD.
b) Chứng minh:AD\(^2\)=DH.DB.
c)Tính độ dài các đoạn thẳng AH,DH.
d) Tính tỉ số diện tích \(\Delta\)HAD và \(\Delta\)ABD từ đó suy ra tỉ số đồng dạng của nó.
giúp mình với mai mình thi rồi SOS !!!!!!!
2:
a: =>x-4>=0
=>x>=4
b: =>x+1>0
=>x>-1

[Lớp 8]
Bài 1. Giải phương trình sau đây:
a) \(7x+1=21;\)
b) \(\left(4x-10\right)\left(24+5x\right)=0;\)
c) \(\left|x-2\right|=2x-3;\)
d) \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}.\)
Bài 2. Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số:
\(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}.\)
Bài 3. Tìm giá trị lớn nhất của \(A=-x^2+2x+9.\)
Bài 4. Giải bài toán bằng cách lập phương trình:
Một người đi xe máy dự định đi từ A đến B với vận tốc 36km/h. Nhưng khi thực hiện người đó giảm vận tốc 6km/h nên đã đến B chậm hơn dự định là 24 phút.
Tính quãng đường AB.
Bài 5. Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD⊥ AB (D ∈ AB), HE ⊥ AC (E∈ AC). AB=12cm, AC=16cm.
a) Chứng minh: ΔHAC đồng dạng với ΔABC;
b) Chứng minh AH2=AD.AB;
c) Chứng minh AD.AB=AE.AC;
d) Tính \(\dfrac{S_{ADE}}{S_{ABC}}.\)
Bài 4 :
24 phút = \(\dfrac{24}{60} = \dfrac{2}{5}\) giờ
Gọi thời gian dự định đi từ A đến B là x(giờ) ; x > 0
Suy ra quãng đường AB là 36x(km)
Khi vận tốc sau khi giảm là 36 -6 = 30(km/h)
Vì giảm vận tốc nên thời gian đi hết AB là x + \(\dfrac{2}{5}\)(giờ)
Ta có phương trình:
\(36x = 30(x + \dfrac{2}{5})\\ \Leftrightarrow x = 2\)
Vậy quãng đường AB dài 36.2 = 72(km)
Bài 3 :
\(A = -x^2 + 2x + 9 = -(x^2 -2x - 9) \\= -(x^2 - 2x + 1 + 10) = -(x^2 -2x + 1)+ 10\\=-(x-1)^2 + 10\)
Vì : \((x-1)^2 \geq 0\) ∀x \(\Leftrightarrow -(x-1)^2 \)≤ 0 ∀x \(\Leftrightarrow -(x-1)^2 + 10\) ≤ 10
Dấu "=" xảy ra khi và chỉ khi x - 1 = 0 ⇔ x = 1
Vậy giá trị nhỏ nhất của A là 10 khi x = 1
giải các bất phương trình sau
a)\(\dfrac{2-x}{3}< \dfrac{3-2x}{5}\)
b)\(\dfrac{2x+15}{9}\ge\dfrac{x-1}{5}+\dfrac{x}{3}\)
a: =>5(2-x)<3(3-2x)
=>10-5x<9-6x
=>x<-1
b: =>2/9x+5/3>=1/5x-1/5+1/3x
=>2/9x+5/3>=8/15x-1/5
=>-14/45x>=-28/15
=>x<=6
Giải các bất phương trình sau
1) \(\dfrac{\text{x - 2}}{x+1}-\dfrac{3}{x+2}>0\) 2) \(\dfrac{\text{x + 1}}{x+2}+\dfrac{x}{x-3}\le0\)
3) \(\dfrac{\text{x}^2+2x+5}{x+4}>x-3\) 4) \(\sqrt{\text{x^2}-3x+2}\ge3\)
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
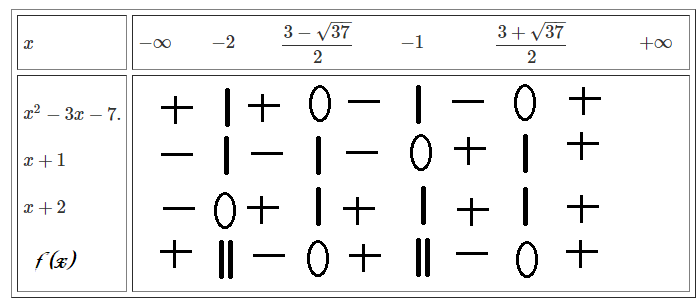
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)