rút gọn
\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\) (a\(\ge\)0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Rút gọn các biểu thức sau:
A = \(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{a}\); \(a>0\)
B = \(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{5a};a\ge0\)
1, Rút gọn
A=\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\: \sqrt{a}\)
Với a\(\ge\)0
Với a\(\ge\)0,ta có
A=\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)
A=\(3\sqrt{5a}-\sqrt{4.5a}+4\sqrt{9.5a}+\sqrt{a}\)
A=\(3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
A=\(13\sqrt{5a}+\sqrt{a}\)
Lời giải:
\(A=3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}=3\sqrt{5}.\sqrt{a}-\sqrt{4}.\sqrt{5}.\sqrt{a}+4.\sqrt{9}.\sqrt{5}.\sqrt{a}+\sqrt{a}\)
\(=3\sqrt{5}.\sqrt{a}-2\sqrt{5}\sqrt{a}+12\sqrt{5}.\sqrt{a}+\sqrt{a}\)
\(=\sqrt{a}(3\sqrt{5}-2\sqrt{5}+12\sqrt{5}+1)=\sqrt{a}(13\sqrt{5}+1)\)
Rút gọn: (Giải chi tiết từng bước)
9) \(2\sqrt{8\sqrt{3}-2\sqrt{5\sqrt{3}}}-3\sqrt{20\sqrt{3}}\)
10) \(\sqrt{12x}-\sqrt{48x}-3\sqrt{3x}+27\) với x \(\ge\) 0
11) \(\sqrt{18x}-5\sqrt{8x}+7\sqrt{18x}+28\) với \(x\ge0\)
12) \(\sqrt{45a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\) với \(a\ge0\)
Cần gấp ạ
9) Sửa: \(2\sqrt{8\sqrt{3}}-2\sqrt{5\text{ }\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
\(=2\sqrt{2^2\cdot2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{2^2\cdot5\sqrt{3}}\)
\(=2\cdot2\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\cdot2\sqrt{5\sqrt{3}}\)
\(=4\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
\(=4\sqrt{2\sqrt{3}}-8\sqrt{5\sqrt{3}}\)
10) \(\sqrt{12x}-\sqrt{48x}-3\sqrt{3x}+27\)
\(=\sqrt{2^2\cdot3x}-\sqrt{4^2\cdot3x}-3\sqrt{3x}+27\)
\(=2\sqrt{3x}-4\sqrt{3x}-3\sqrt{3x}+27\)
\(=-5\sqrt{3x}++27\)
11) \(\sqrt{18x}-5\sqrt{8x}+7\sqrt{18x}+28\)
\(=\sqrt{3^2\cdot2x}-5\sqrt{2^2\cdot2x}+7\sqrt{3^2\cdot2x}+28\)
\(=3\sqrt{2x}-5\cdot2\sqrt{2x}+7\cdot3\sqrt{2x}+28\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28\)
\(=14\sqrt{2x}+28\)
12) \(\sqrt{45a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)
\(=\sqrt{3^2\cdot5a}-\sqrt{2^2\cdot5a}+4\sqrt{3^2\cdot5a}+\sqrt{a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+4\cdot3\sqrt{5a}+\sqrt{a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
\(=13\sqrt{5a}+\sqrt{a}\)
Bài 1 rút gọn
a)\(3\sqrt{5a}-\sqrt{20a}+\sqrt{45a}\)với a
≥0
b)\(\sqrt{160a^2}+\dfrac{1}{2}\sqrt{40a^2}-3\sqrt{90a^2}\)
c)\(\sqrt{x^2-2x+1}-\sqrt{x^2-4x+4}\)
giải hộ mik
a: Ta có: \(3\sqrt{5a}-\sqrt{20a}+\sqrt{45a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+3\sqrt{5a}\)
\(=4\sqrt{5a}\)
b: Ta có: \(\sqrt{160a^2}+\dfrac{1}{2}\sqrt{40a^2}-3\sqrt{90a^2}\)
\(=4a\sqrt{10}+\dfrac{1}{2}\cdot2a\sqrt{10}-3\cdot3a\sqrt{10}\)
\(=-4a\sqrt{10}\)
c: Ta có: \(\sqrt{x^2-2x+1}-\sqrt{x^2-4x+4}\)
\(=\left|x-1\right|-\left|x-2\right|\)
Rút gon các bt sau
A=\(\sqrt{12}\)+2\(\sqrt{27}\)-3\(\sqrt{48}\)
C=\(\sqrt{20a}\)+4\(\sqrt{45a}\)-2\(\sqrt{125a}\)với a≥0
a) Ta có: \(A=\sqrt{12}+2\sqrt{27}-3\sqrt{48}\)
\(=2\sqrt{3}+6\sqrt{3}-12\sqrt{3}\)
\(=-4\sqrt{3}\)
b) Ta có: \(C=\sqrt{20a}+4\sqrt{45a}-2\sqrt{125a}\)
\(=2\sqrt{5a}+12\sqrt{5a}-10\sqrt{5a}\)
\(=4\sqrt{5a}\)
Bài 20 (trang 15 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $\sqrt{\dfrac{2a}{3}}.\sqrt{\dfrac{3a}{8}}$ với $a\ge 0$ ; b) $\sqrt{13a}.\sqrt{\dfrac{52}{a}}$ với $a>0$ ;
c) $\sqrt{5a}.\sqrt{45a}-3a$ với $a\ge 0$ ; d) $(3-a)^2-\sqrt{0,2}.\sqrt{180a^2}$.
a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
a) Ta có:
b) Ta có:
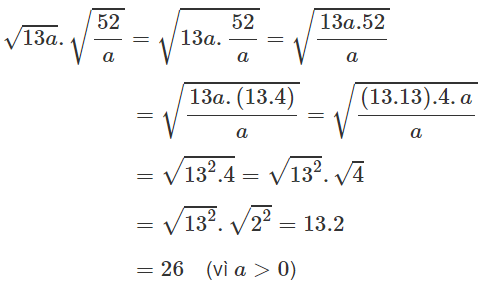
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
d) Ta có:
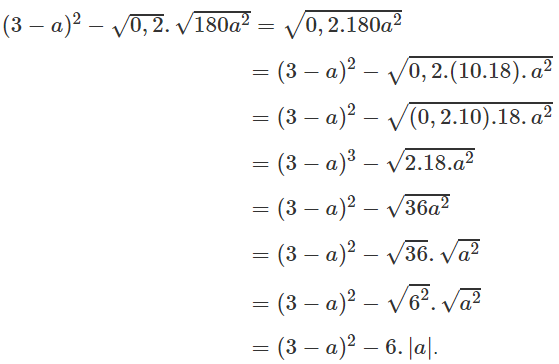
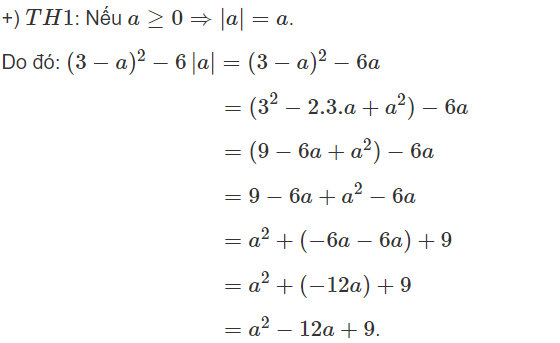
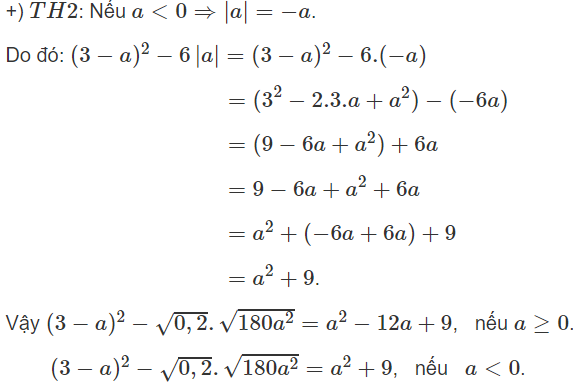
b) \(\sqrt{13a}\).\(\sqrt{\frac{52}{a}}\)=\(\sqrt{13a.\frac{52}{a}}\)=\(\sqrt{13.13.2.2}\)=13.2=26
rút gọn các biểu thức:
a,\(6\sqrt{a}+\dfrac{2}{3}\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{9}{a}}+\sqrt{7}vớia>0\)
b,\(5a\sqrt{25ab^3}\sqrt{3}\sqrt{12a^3b^3}+9ab\sqrt{9ab}-5b\sqrt{81a^3b}vớia,b>0\)
c,\(\sqrt{\dfrac{a}{b}}+\sqrt{ab}-\dfrac{a}{b}\sqrt{\dfrac{b}{a}}vớia,b>0\)
d,\(11\sqrt{5a}-\sqrt{125a}+\sqrt{20a}-4\sqrt{45a}+9\sqrt{a}vớia>0\)
Bạn làm đc bài này chưa chỉ mình với
a: \(=6\sqrt{a}+\dfrac{1}{3}\sqrt{a}-3\sqrt{a}+\sqrt{7}=\dfrac{10}{3}\sqrt{a}+\sqrt{7}\)
b: \(=5a\cdot5b\sqrt{ab}+\sqrt{3}\cdot2\sqrt{3}\cdot ab\sqrt{ab}+9ab\cdot3\sqrt{ab}-5b\cdot9a\sqrt{ab}\)
\(=25ab\sqrt{ab}+12ab\sqrt{ab}+27ab\sqrt{ab}-45ab\sqrt{ab}\)
\(=19ab\sqrt{ab}\)
c: \(=\dfrac{\sqrt{ab}}{b}+\sqrt{ab}-\dfrac{a}{b}\cdot\dfrac{\sqrt{b}}{\sqrt{a}}\)
\(=\sqrt{ab}\left(\dfrac{1}{b}+1\right)-\dfrac{\sqrt{a}}{\sqrt{b}}\)
\(=\sqrt{ab}\)
d: \(=11\sqrt{5a}-5\sqrt{5a}+2\sqrt{5a}-12\sqrt{5a}+9\sqrt{a}\)
\(=-4\sqrt{5a}+9\sqrt{a}\)
1) \(\sqrt{9a^2.b^2}\) với a<0, b<0
2) \(\sqrt{3a}.\sqrt{27a}\) với a \(\ge\)0
3) \(\sqrt{3a^5}.12a\) với a>0
4) \(\sqrt{5a}.\sqrt{45a}-3a\) ( với a ≥ 0)
5) \(\sqrt{3+\sqrt{a}}\).\(\sqrt{3-\sqrt{a}}\)
6) \(\sqrt{3+\sqrt{5}}\). \(\sqrt{3\sqrt{5}}\)
\(1) \sqrt{9a^2.b^2}\)=3ab
\(2) \sqrt{3a}.\sqrt{27a}=\sqrt{3a}.3\sqrt{3a}=9a\)
\(3) \sqrt{3a^5}.12a=12\sqrt{3a^7}\)
\(4) \sqrt{5a}.\sqrt{45a}-3a=15a-3a=12a\)
\(5) \sqrt{3+\sqrt{a}}.\sqrt{3-\sqrt{a}}=\sqrt{(3+\sqrt{a}).(3-\sqrt{a})} =\sqrt{9-a} \)
\(6) \sqrt{3+\sqrt{5}}.\sqrt{3\sqrt{5}} =\sqrt{\sqrt{3\sqrt{5}}.(3+\sqrt{5})} =\sqrt{9+\sqrt{15}}\)
1) \(\sqrt{9a^2b^2}=3ab\)
2) \(\sqrt{3a}\cdot\sqrt{27a}=9a\)
4) \(\sqrt{5a}\cdot\sqrt{45a}-3a=15a-3a=12a\)
Rút gọn:
a,\(\sqrt{4\left(a-3\right)^2}\)với a \(\ge\)3
b,\(\sqrt{9\left(b-2\right)^2}\)với b < 2
c,\(\sqrt{27.48\left(1-a\right)^2}\)với a > 1
d,\(\sqrt{5a}.\sqrt{45a}-3a\)với a \(\ge\)0
e,\(\frac{\sqrt{48x^3}}{\sqrt{3x^5}}\)với x > 0
a) \(\sqrt{4\left(a-3\right)^2}=\sqrt{2^2\left(a-3\right)^2}=2\sqrt{\left(a-3\right)^2}=2.\left|a-3\right|=2\left(a-3\right)=2a-6\) (Vì \(a\ge3\) )
b) \(\sqrt{9\left(b-2\right)^2}=\sqrt{3^2\left(b-2\right)^2}=3\sqrt{\left(b-2\right)^2}=3\left|b-2\right|=3\left(2-b\right)\)
\(=6-3b\) (vì b < 2 )
b) \(\sqrt{27.48\left(1-a\right)^2}=\sqrt{27.3.16.\left(1-a\right)^2}=\sqrt{81.16.\left(1-a\right)^2}\)
\(=\sqrt{9^2.4^2.\left(1-a\right)^2}=9.4\sqrt{\left(1-a\right)^2}=36.\left|1-a\right|=36\left(1-a\right)=36-36a\) (vì a > 1)
a) \(\sqrt{4\left(a-3\right)^2}=2.\left|a-3\right|=2\left(a-3\right)\)
b) \(\sqrt{9\left(b-2\right)^2}=3.\left|b-2\right|=3\left(2-b\right)\)
c) \(\sqrt{27.48\left(1-a\right)^2}=36.\left|1-a\right|=36\left(a-1\right)\)
d) \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{5a.45a}-3a=15a-3a=12a\)
e) \(\frac{\sqrt{48x^3}}{\sqrt{3x^5}}=\sqrt{\frac{48x^3}{3x^5}}=\sqrt{\frac{16}{x^2}}=\frac{4}{x}\)