Chứng minh sin\(\dfrac{A}{2}< =\dfrac{BC}{AC+AB}\)
TN
Những câu hỏi liên quan
Cho tam giác ABC có BC=a, AC=b, AB=c. chứng minh: \(sin\dfrac{A}{2}< =\dfrac{a}{b+c}\)
Hình tự vẽ nha
Kẻ phân giác \(AD,BK\perp AD\)
\(\sin\dfrac{A}{2}=\sin BAD\)
xét \(\Delta AKB\) vuông tại K,có:
\(\sin BAD=\dfrac{BK}{AB}\left(1\right)\)
Xét \(\Delta BKD\) vuông tại K,có :
\(BK\le BD\) thay vào (1):
\(\sin BAD\le\dfrac{BD}{AB}\left(2\right)\)
lại có:\(\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{BD}{BD+CD}=\dfrac{AB}{AB+AC}\)
\(\Rightarrow\dfrac{BD}{BC}=\dfrac{AB}{AB+AC}\)
\(\Rightarrow BD=\dfrac{AB\cdot AC}{AB+AC}\) thay vào (2)
\(\sin BAD\le\dfrac{\dfrac{AB\cdot AC}{AB+AC}}{AB}=\dfrac{BC}{AB+AC}\)
\(\RightarrowĐPCM\)
Tick plz
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A , tia phân giác của widehat{BAC} cắt BC tại D . Gọi E , F lần lượt là hình chiếu vuông góc của D trên AB;AC. Đặt AC a , AB c , BC a, AD d
a , Chứng minh : dfrac{sqrt{2}}{d} dfrac{1}{b} + dfrac{1}{c}
b , Chứng minh : dfrac{1}{sindfrac{A}{2}} + dfrac{1}{sindfrac{B}{2}}+ dfrac{1}{sindfrac{C}{2}} 6
Đọc tiếp
Cho tam giác ABC vuông tại A , tia phân giác của \(\widehat{BAC}\) cắt BC tại D . Gọi E , F lần lượt là hình chiếu vuông góc của D trên AB;AC. Đặt AC = a , AB = c , BC= a, AD = d
a , Chứng minh : \(\dfrac{\sqrt{2}}{d}\) = \(\dfrac{1}{b}\) + \(\dfrac{1}{c}\)
b , Chứng minh : \(\dfrac{1}{sin\dfrac{A}{2}}\) + \(\dfrac{1}{sin\dfrac{B}{2}}\)+ \(\dfrac{1}{sin\dfrac{C}{2}}\) > 6
Cho tam giác ABC có 3 góc nhọn, \(AB=c,AC=b,BC=a\)
Chứng minh: \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
Lời giải:
Kẻ \(BE\perp AC(E\in AC)\)
Khi đó \(\sin A=\frac{BE}{c}\Rightarrow \frac{a}{\sin A}=\frac{ac}{BE}\)
Mặt khác, \(S_{ABC}=\frac{BE.b}{2}\Rightarrow BE=\frac{2S_{ABC}}{b}\)
\(\Rightarrow \frac{a}{\sin A}=\frac{abc}{2S_{ABC}}\). Hoàn toàn tương tự với \(\frac{b}{\sin B},\frac{c}{\sin C}\) ta có:
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{abc}{2S_{ABC}}\) (đpcm)
Đúng 0
Bình luận (0)
Gọi O là đường tròn ngoại tiếp tam giác ABC, D là trung điểm của BC, ta có:
\(OD\perp BC\)
\(OB=R;BD=\dfrac{1}{2}a\)
\(\widehat{BOD}=\widehat{A}\) (A là góc nội tiếp chắn cung BC, Ở là góc tâm chắn \(\dfrac{1}{2}\) cung BC)
Trong tam giác vuông DOB ta có:
\(sin\left(DOB\right)=\dfrac{BD}{OB}\)
\(\Rightarrow sinA=\dfrac{1}{2}\cdot\dfrac{a}{R}\Rightarrow\dfrac{a}{sinA}=2R\)
Chứng minh tương tự ta có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\)
Đúng 0
Bình luận (0)
Kẻ AH, BE là đường cao của tam giác ABC.
Xét tam giác ABH vuông tại H có:
\(\sin B=\dfrac{AH}{AB}=\dfrac{AH}{c}\) (tỉ số lượng giác của góc nhọn)
\(\Rightarrow AH=c.\sin B\) (1)
Xét tam giác ACH vuông tại H có:
\(\sin C=\dfrac{AH}{AC}=\dfrac{AH}{b}\) (tỉ số lượng giác của góc nhọn)
\(\Rightarrow AH=b.\sin C\) (2)
Từ (1) và (2) \(\Rightarrow c.\sin B=b.\sin C\)
\(\Rightarrow\dfrac{c}{\sin C}=\dfrac{b}{\sin B}\) (3)
Xét tam giác ABE vuông tại E có:
\(\sin A=\dfrac{BE}{AB}=\dfrac{BE}{c}\) (tỉ số lượng giác)
\(\Rightarrow BE=c.\sin A\) (4)
Xét tam giác BEC vuông tại E có:
\(\sin C=\dfrac{BE}{BC}=\dfrac{BE}{a}\) (tỉ số lượng giác)
\(\Rightarrow BE=a.\sin C\) (5)
Từ (4) và (5) \(\Rightarrow c.\sin A=a.\sin C\)
\(\Rightarrow\dfrac{c}{\sin C}=\dfrac{a}{\sin A}\) (6)
Từ (3) và (6) \(\Rightarrow\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC a, CA b, AB c, đường cao AH.a) Chứng minh: 1+tam^2Bdfrac{1}{cos^2B};tandfrac{C}{2}dfrac{c}{a+b}b) Chứng minh: AH a. sin B. cos B, BHa·cos2B, CHa·sin2Bc) Lấy D trên cạnh AC. Kẻ DE vuông góc BC tại E. Chứng minh:sinBdfrac{ABcdot AD+EBcdot ED}{ABcdot BE+DAcdot DE} (
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = a, CA = b, AB = c, đường cao AH.
a) Chứng minh: \(1+tam^2B=\dfrac{1}{cos^2B};tan\dfrac{C}{2}=\dfrac{c}{a+b}\)
b) Chứng minh: AH = a. sin B. cos B, BH=a·cos2B, CH=a·sin2B
c) Lấy D trên cạnh AC. Kẻ DE vuông góc BC tại E. Chứng minh:
sinB=\(\dfrac{AB\cdot AD+EB\cdot ED}{AB\cdot BE+DA\cdot DE}\) (
a) \(1+tan^2B=1+\dfrac{AC^2}{AB^2}=\dfrac{AB^2+AC^2}{AB^2}=\dfrac{BC^2}{AB^2}=\dfrac{1}{\left(\dfrac{AB}{BC}\right)^2}=\dfrac{1}{cos^2B}\)
b) Ta có: \(a.sinB.cosB=BC.\dfrac{AC}{BC}.\dfrac{AB}{BC}=\dfrac{AC.AB}{BC}=\dfrac{AH.BC}{BC}=AH\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=BC.\left(\dfrac{AB}{BC}\right)^2=BC.cos^2B\)
Tương tự \(\Rightarrow CH=BC.sin^2B\)
Đúng 2
Bình luận (0)
Cho tam giác ABC; AB c; AC b; BC a; đường phân giác AD. Chứng minh:
1) sindfrac{A}{2}ledfrac{a}{b+c}
2) sindfrac{A}{2}+sindfrac{B}{2}+sindfrac{C}{S} 2
3) dfrac{1}{sindfrac{A}{2}}+dfrac{1}{sindfrac{B}{2}}+dfrac{1}{sindfrac{C}{2}}ge6
4) sindfrac{A}{2}+sindfrac{B}{2}+sindfrac{C}{2}ledfrac{1}{8}
5) dfrac{1}{sin^2dfrac{A}{2}}+dfrac{1}{sin^2dfrac{B}{2}}+dfrac{1}{sin^2dfrac{C}{2}}ge12
Đọc tiếp
Cho tam giác ABC; AB = c; AC = b; BC = a; đường phân giác AD. Chứng minh:
1) \(\sin\dfrac{A}{2}\le\dfrac{a}{b+c}\)
2) \(\sin\dfrac{A}{2}+\sin\dfrac{B}{2}+\sin\dfrac{C}{S}< 2\)
3) \(\dfrac{1}{\sin\dfrac{A}{2}}+\dfrac{1}{\sin\dfrac{B}{2}}+\dfrac{1}{\sin\dfrac{C}{2}}\ge6\)
4) \(\sin\dfrac{A}{2}+\sin\dfrac{B}{2}+\sin\dfrac{C}{2}\le\dfrac{1}{8}\)
5) \(\dfrac{1}{\sin^2\dfrac{A}{2}}+\dfrac{1}{\sin^2\dfrac{B}{2}}+\dfrac{1}{\sin^2\dfrac{C}{2}}\ge12\)
1)
Kẻ phân giác AD,BK vuông góc với AD
sin A/2=sinBAD
xét tam giác AKB vuông tại K,có:
sinBAD=BK/AB (1)
xét tam giác BKD vuông tại K,có
BK<=BD thay vào (1):
sinBAD<=BD/AB(2)
lại có:BD/CD=AB/AC
=>BD/(BD+CD)=AB/(AB+AC)
=>BD/BC=AB/(AB+AC)
=>BD=(AB*BC)/(AB+AC) thay vào (2)
sinBAD<=[(AB*BC)/(AB+AC)]/AB
= BC/(AB + AC)
=>ĐPCM
Đúng 0
Bình luận (0)
Bài 2: Cho ΔABC vuông tại A
a) Chứng minh: \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
b) Chứng minh: \(BC^2=AB^2+AC^2-2.AB.AC.cosA\)
a) Xét ΔABC vuông tại A có
\(\left\{{}\begin{matrix}\sin\widehat{A}=\dfrac{BC}{BC}=1\\\sin\widehat{B}=\dfrac{AC}{BC}\\\sin\widehat{C}=\dfrac{AB}{BC}\end{matrix}\right.\)
Ta có: \(\dfrac{BC}{\sin\widehat{A}}=\dfrac{BC}{1}=BC\)
\(\dfrac{AC}{\sin\widehat{B}}=\dfrac{AC}{\dfrac{AC}{BC}}=BC\)
\(\dfrac{AB}{\sin\widehat{C}}=\dfrac{AB}{\dfrac{AB}{BC}}=BC\)
Do đó: \(\dfrac{BC}{\sin\widehat{A}}=\dfrac{AC}{\sin\widehat{B}}=\dfrac{AB}{\sin\widehat{C}}\)
b) Ta có: \(2\cdot AB\cdot AC\cdot\cos\widehat{A}\)
\(=2\cdot AB\cdot AC\cdot0\)
=0
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=AB^2+AC^2+2\cdot AB\cdot AC\cdot\cos\widehat{A}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có BC = a ; CA = b ; AB = c. Chứng minh rằng:
a) \(sin\dfrac{A}{2}\)≤\(\dfrac{a}{b+c}\)
b) \(\sin\dfrac{A}{2}.\sin\dfrac{B}{2}.\sin\dfrac{C}{2}\) ≤ \(\dfrac{1}{8}\)
a, Vẽ phân giác AD của góc BAC
Kẻ BH\(\perp\)AD tại H ; CK\(\perp AD\) tại K
Dễ thấy \(sin\widehat{A_1}=sin\widehat{A_2}=sin\dfrac{A}{2}=\dfrac{BH}{AB}=\dfrac{CK}{AC}=\dfrac{BH+CK}{AB+AC}\le\)\(\le\dfrac{BD+CD}{b+c}=\dfrac{a}{b+c}\)
b, Tượng tự \(sin\dfrac{B}{2}\le\dfrac{b}{a+c};sin\dfrac{C}{2}\le\dfrac{c}{a+b}\)
Mặt khác \(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ca}=8abc\)
\(\Rightarrow sin\dfrac{A}{2}.sin\dfrac{B}{2}.sin\dfrac{C}{2}\le\dfrac{abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\dfrac{1}{8}\)
Đúng 0
Bình luận (0)
cho tg ABC\(\perp\)A, đường phân giác BD.
CMR: a) \(\tan\dfrac{B}{2}=\dfrac{AC}{BC+AB}\)
CMR: b) S(ABC)=\(\dfrac{AB\times BC}{2}\times\sin B\)
b: \(\dfrac{AB\cdot BC}{2}\cdot sinB\)
\(=\dfrac{AB\cdot BC}{2}\cdot\dfrac{AC}{BC}=\dfrac{AB\cdot AC}{2}\)
\(=S_{ABC}\)
a: Xét ΔABD vuông tại A có tan ABD=AD/AB
Xét ΔCBA có BD là phân giác
nên AD/AB=CD/BC
=>\(\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{AD+CD}{AB+BC}=\dfrac{AC}{AB+BC}\)
=>\(tan\left(ABD\right)=\dfrac{AC}{AB+BC}\)
Đúng 0
Bình luận (0)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\) Chứng minh \(\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}\) = 3
Phần chứng minh (*) khá quen thuộc, áp dụng phân tích đa thức thành nhân tử và kiến thức chuyển vế, bạn có thể tham khảo thêm
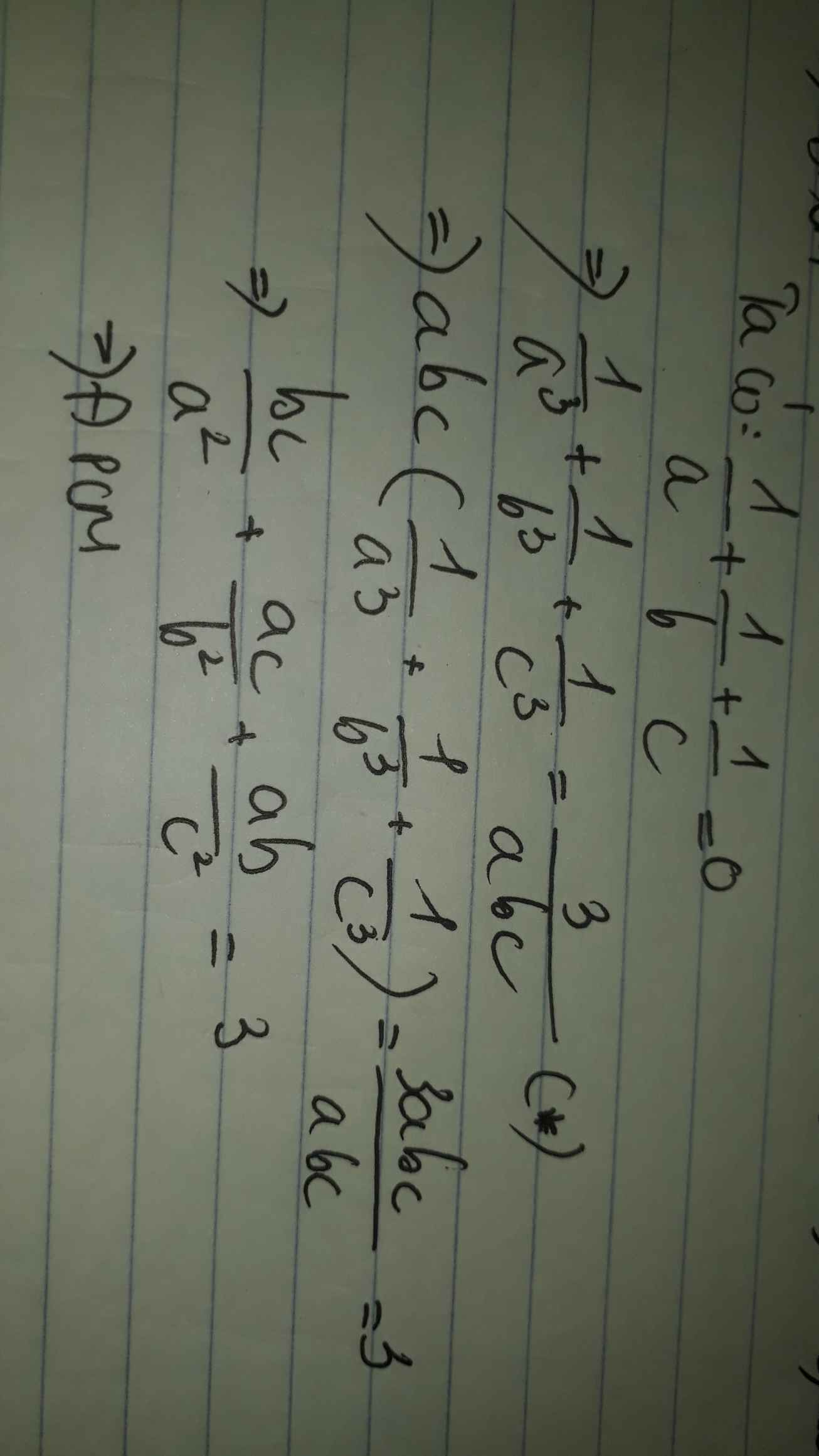
Đúng 1
Bình luận (0)




