Tìm giá trị của \(a\) và \(b\) để đường thẳng \(ax-by=4\) đi qua hai điểm \(A\left(4;3\right),B\left(-6;-7\right)\)?
SK
Những câu hỏi liên quan
Tìm giá trị của a và b để đường thẳng ax – by = 4 đi qua hai điểm A(4; 3), B(-6; -7)
Đường thẳng ax – by = 4 đi qua hai điểm A(4; 3), B(-6; -7) nên tọa độ của A và B nghiệm đúng phương trình đường thẳng.
*Với điểm A: 4a – 3b = 4
*Với điểm B: -6a + 7b = 4
Hai số a và b là nghiệm của hệ phương trình: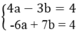
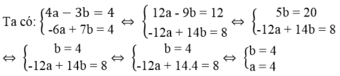
Vậy a = 4, b = 4.
Đúng 0
Bình luận (0)
Phần tự luận
Nội dung câu hỏi 1
a)Tìm giá trị của a và b để đường thẳng ax + by = 4 đi qua hai điểm A(4;-3) và B(-6;7).
Tìm các giá trị của a và b để đường thẳng ax-by=4 đi qua 2 điểm A(4:3) và B(-6:-7)
Vì đường thẳng ax-by=4 đi qua 2 điểm A(4;3) và B(-6;-7)
nên 4a-3b=4 và -6a-(-7)b=4
3(4a-3b)=12 và 2(-6a+7b)=8
12a-9b=12 và -12a+14b=8
5b=20 và 4a-3b=4
b=4 và a=4
Giúp mk thanhyou my bạn nhiều Bài 1 tìm gia trị của mĐể 2 đường thẳng (d1) 5x-2y 3 ,(d2) x+ym cách nhau tại một điểm trên truc oy vẽ hai điểm này trên một mặt phẳng toạ đoĐể 2 đường thẳng (d1 mx +3y 10, d2 x-2y 4 7cat nhau tại một điểm trên truc ox ve hai đường thẳng này trên cùng một mặt phẳng toạ đo Bài 2 tìm hai số ạ, b sao cho 5a -4b -5 và dường thang ax+by 4 đi qua điểm A(-7,4)Bài 3 tim giá trị của ab để duong thẳng ax-by4 đi qua 2 điểm A (4,3) B(-6,-7)
Đọc tiếp
Giúp mk thanhyou my bạn nhiều
Bài 1 tìm gia trị của m
Để 2 đường thẳng (d1) 5x-2y =3 ,(d2) x+y=m cách nhau tại một điểm trên truc oy vẽ hai điểm này trên một mặt phẳng toạ đo
Để 2 đường thẳng (d1 mx +3y =10, d2 x-2y =4 7cat nhau tại một điểm trên truc ox ve hai đường thẳng này trên cùng một mặt phẳng toạ đo
Bài 2 tìm hai số ạ, b sao cho 5a -4b =-5 và dường thang ax+by =4 đi qua điểm A(-7,4)
Bài 3 tim giá trị của ab để duong thẳng ax-by=4 đi qua 2 điểm A (4,3) B(-6,-7)
a) Tìm các giá trị của a và b để đường thẳng (d): yax+b đi qua hai điểm M(1;5) và N(2;8).b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y 2x – a + 1 và parabol (P): y dfrac{1}{2}x^2.1.Tìm a để đường thẳng a đi qua điểm A (-1;3)2.Tìm a để (d) cắt (P) tại hai điểm phân biệt có tọa độ (x_1;x_2) và (x_2;y_2) thỏa mãn điều kiện x_1x_2left(y_1+y_2right)+480
Đọc tiếp
a) Tìm các giá trị của a và b để đường thẳng (d): y=ax+b đi qua hai điểm M(1;5) và N(2;8).
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = 2x – a + 1 và parabol (P): y = \(\dfrac{1}{2}x^2\).
1.Tìm a để đường thẳng a đi qua điểm A (-1;3)
2.Tìm a để (d) cắt (P) tại hai điểm phân biệt có tọa độ (\(x_1;x_2\)) và (\(x_2;y_2\)) thỏa mãn điều kiện \(x_1x_2\left(y_1+y_2\right)+48=0\)
a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
b:
1: Thay x=-1 và y=3 vào (d), ta được:
\(2\cdot\left(-1\right)-a+1=3\)
=>-a-1=3
=>-a=4
hay a=-4
Đúng 2
Bình luận (0)
Tìm hai số a và b sao cho 5a – 4b = -5 và đường thẳng: ax + by = -1 đi qua điểm A(-7; 4).
Đường thẳng ax + by = -1 đi qua điểm A(-7; 4) nên tọa độ của A nghiệm đúng phương trình đường thẳng.
Ta có: a.(-7) + b.4 = -1
Khi đó ta có phương trình: 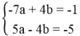
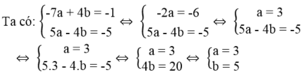
Vậy a = 3, b = 5.
Đúng 0
Bình luận (0)
Giải hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\)
Tìm giá trị của a và b để phương trình ax - by = 4 đi qua 2 điểm A(2;3) và B(-1;2)
Bài 1:
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\)
Bài 2:
Theo đề, ta có:
\(\left\{{}\begin{matrix}2a-3b=4\\-a-2b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a-3b=4\\-2a-4b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{12}{7}\\a=-\dfrac{4}{7}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trên mặt phẳng Oxy, cho đường thẳng \(\Delta:x-y+2=0,\Delta':ax+by-2=0\left(-2\le b\le2\right)\) và điểm A (1;1). Tính giá trị của \(T=a^2+b^2\) biết \(\Delta'\) đi qua A và \(\cos\left(\Delta;\Delta'\right)\) đạt giá trị lớn nhất
Tìm các giá trị của a và b để đường thẳng y=ax+b đi qua điểm M ( 3;-5), N ( -1;3/2)
Vì đường thẳng y = ax + b đi qua điểm ( 3;-5 )
=> -5 = 3a + b
Vì đường thẳng y = ax + b đi qua điểm ( -1 ; 3/2 )
=> 3/2 = -a + b
Giải hệ phương trình :
3a + b = -5
-a + b = 3/2
Ta có : 3a + b - ( -a + b ) = 3a + b + a - b = 4a = -5 - 3/2 = -13/2
=> a = -13/2 : 4 = -13/8
Thay a = -13/8 vào - a + b = 3/2 ta được :
13/8 + b = 3/2
=> b = 3/2 - 13/8 = -1/8
Vậy a = -13/8 ; b = -1/8
Đúng 0
Bình luận (0)
Vì đường thẳng y = ax + b đi qua điểm ( 3;-5 )
=> -5 = 3a + b
Vì đường thẳng y = ax + b đi qua điểm ( -1 ; 3/2 )
=> 3/2 = -a + b
Giải hệ phương trình :
3a + b = -5
-a + b = 3/2
Ta có : 3a + b - ( -a + b ) = 3a + b + a - b = 4a = -5 - 3/2 = -13/2
=> a = -13/2 : 4 = -13/8
Thay a = -13/8 vào - a + b = 3/2 ta được :
13/8 + b = 3/2
=> b = 3/2 - 13/8 = -1/8
Vậy a = -13/8 ; b = -1/8
Đúng 0
Bình luận (0)



