Chứng minh rằng số đo góc của hình n - giác đều là \(\dfrac{\left(n-2\right).180^0}{n}\)
SK
Những câu hỏi liên quan
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là widehat{A}_1+widehat{A}_2+widehat{A}_3+.....+widehat{A}_nleft(n-2right).180^0. Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là dfrac{left(n-2right).180^0}{n}, vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
Đọc tiếp
Điền vào chỗ trống trong các câu sau :
a) Biết rằng tổng số đo các góc của một đa giác n cạnh là \(\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+.....+\widehat{A}_n=\left(n-2\right).180^0\). Vậy tổng số đo các góc của một đa giác 7 cạnh là .......
b) Đa giác đều là đa giác có .....
c) Biết rằng số đo mỗi góc của một đa giác đều n cạnh là \(\dfrac{\left(n-2\right).180^0}{n}\), vậy :
Số đo mỗi góc của ngũ giác đều là ..............
Số đo mỗi góc của lục giác đều là ..............
a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)
Đúng 0
Bình luận (0)
Chứng minh rằng số đo góc của n-giác đều là
\(\frac{\left(n-2\right).180^o}{n}\)
tai vi cu n giac tao thanh n-2 tam giac
Đúng 0
Bình luận (0)
Chứng minh rằng số đo góc của hình n-giác đều là ( n- 2). 1800
Đúng 0
Bình luận (0)
a) Chứng minh tổng số đo các góc trong của một hình
n - giác là (n - 2)180°.
b) Tính tổng số đo các góc của một đa giác 12 cạnh.
a)Vẽ các đường chéo xuất phát từ một đỉnh của n - giác, ta được (n - 2) tam giác.
Tổng các góc của hình n - giác bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800.
b) ta có: (n - 2).1800 = (12 - 2 ).1800 = 18000
Đúng 0
Bình luận (0)
Chứng minh rằng số đo của một hình n-giác đều là n - 2 . 180 0 n
Vẽ một n-giác lồi, kẻ các đường chéo xuất phát từ một đỉnh của n-giác lồi thì chia đa giác đó thành (n - 2) tam giác.
Tổng các góc của n-giác lồi bằng tổng các góc của (n - 2) tam giác bằng (n - 2).180o.
Hình n-gíác đều có n góc bằng nhau nên số đo mỗi góc bằng:
n - 2 . 180 0 n
Đúng 0
Bình luận (0)
a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác
b) Chứng minh rằng hình - n giác có tất cả \(\dfrac{n\left(n-3\right)}{2}\) đường chéo
chứng minh rằng với mọi số tự nhiên n khác 0 ta đều có:
a) \(\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+....+\dfrac{1}{\left(3n-1\right)\left(3n+2\right)}=\dfrac{n}{6n+4}\)
\(\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{\left(3n-1\right)\left(3n+2\right)}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+...+\dfrac{3}{\left(3n-1\right)\left(3n+2\right)}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{3n-1}-\dfrac{1}{3n+2}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{3n+2}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{3n+2}{6n+4}-\dfrac{2}{6n+4}\right)\)
\(=\dfrac{1}{3}.\dfrac{3n}{6n+4}\)
\(=\dfrac{n}{6n+4}\) ( đpcm )
Vậy...
Đúng 0
Bình luận (0)
LP
21 tháng 8 2023 lúc 20:03
1) Gọi d là tổng độ dài các đường chéo của một đa giác lồi trong mặt phẳng có n đỉnh, n3. Gọi p là chu vi của đa giác đó. Chứng minh rằng
n-3 dfrac{2d}{p} left[dfrac{n}{2}right]left[dfrac{n+1}{2}right]-2
(với left[xright] là số nguyên lớn nhất không vượt quá x)
2) Tìm tất cả các hàm số f:ℕ^∗rightarrowℕ^∗ thỏa mãn điều kiện
fleft(x+fleft(yright)right)y+fleft(x+2022right);forall x,yinℕ^∗
Đọc tiếp
1) Gọi \(d\) là tổng độ dài các đường chéo của một đa giác lồi trong mặt phẳng có \(n\) đỉnh, \(n>3\). Gọi \(p\) là chu vi của đa giác đó. Chứng minh rằng
\(n-3< \dfrac{2d}{p}< \left[\dfrac{n}{2}\right]\left[\dfrac{n+1}{2}\right]-2\)
(với \(\left[x\right]\) là số nguyên lớn nhất không vượt quá \(x\))
2) Tìm tất cả các hàm số \(f:ℕ^∗\rightarrowℕ^∗\) thỏa mãn điều kiện
\(f\left(x+f\left(y\right)\right)=y+f\left(x+2022\right);\forall x,y\inℕ^∗\)
Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là : \(\dfrac{n\left(n-3\right)}{2}\) ?
Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: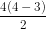 
= 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là 
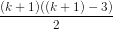Xét đa giác lồi k + 1 cạnh
Nối A1 và Ak, ta được đa giác k cạnh A1A2…Ak có đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.
Vậy số đường chéo của đa giác k + 1 cạnh là
+ k - 2 + 1 =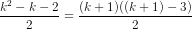 
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh
Đúng 0
Bình luận (0)
Cho 1 hình n-giác .
a) Chứng minh tổng các góc ngoài của hình n- giác bằng ( n - 2 ) . 1800.
b) Tính tổng các góc ngoài của hình n - giác .
a) Vẽ các đường chéo từ đỉnh của n-giác , ta được ( n - 2 ) tam giác .
Tổng các góc của hình n-giác bằng tổng các góc của ( n - 2 ) tam giác và có số đo bằng ( n - 2 ) . 1800
Vậy tổng các góc ngoài của hình n-giác bằng ( n - 2 ) . 1800
b) Tổng số đo của góc trong và góc ngoài tại 1 đỉnh của hình n-giác bằng 1800 . Tổng số đo của góc trong và góc ngoài tại n đỉnh của hình n-giác bằng n.1800 . Tổng các góc của hình n-giác bằng ( n - 2 ) . 1800
Vậy tổng các góc ngoài của hình n-giác bằng : n . 1800 - ( n - 2 ) . 1800 = 3600 .
Đúng 0
Bình luận (0)
Nguyễn Thu Thủy làm đúng rồi nha khỏi làm lại )))
Đúng 0
Bình luận (0)