Chứng minh định lí : Trong các dây của một đường tròn, dây lớn nhất là đường kính
SK
Những câu hỏi liên quan
Chứng minh định lí: Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Giả sử ta có đường tròn đường kính AB = 2R và một dây CD.
Trong ΔCOD, theo bất đẳng thức tam giác ta có:
CD ≤ OC + CD
=> CD ≤ 2R
=> CD ≤ AB (đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng trong một đường tròn, đường kính là dây lớn nhất.
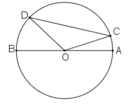
Giả sử CD là một dây của đường tròn bán kính R và AB là một đường kính của nó. Ta có:
- Nếu C, O, D không thẳng hàng thì trong tam giác COD có
CD < OC + OD = 2R = AB.
- Nếu C, O, D thằng hàng thì
CD < OC + OD = R + R = 2R (1)
Do AB là đường kính nên: AB = 2R (2)
Từ (1) và (2) suy ra: CD < AB .
Vậy trong mọi trường hợp ta luôn có đường kính là dây lớn nhất.
Đúng 0
Bình luận (0)
Chứng minh rằng trong một đường tròn, đường kính là dây lớn nhất ?
Giả sử ta có đường tròn tâm O đường kính AB, dây CD khác với đường kính
Vì O,C,D không thẳng hàng
nên DC<OC+OD=2R=AB
=>AB là dây lớn nhất
Đúng 0
Bình luận (0)
1) Chứng minh định lý: " Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy."
2) Chứng minh định lý: " Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy."
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.Hình 29
Đọc tiếp
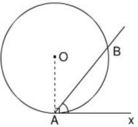
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
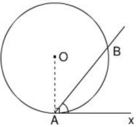
Hình 29
Cách 1: (Chứng minh trực tiếp)
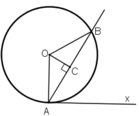
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
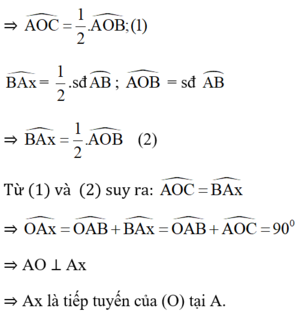
Cách 2: (Chứng minh phản chứng)
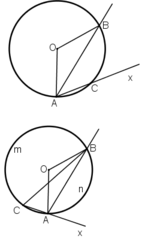
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB

+ C nằm trên cung lớn AB
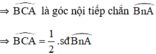
Mà 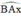 là góc ngoài của tam giác BAC
là góc ngoài của tam giác BAC
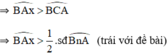
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.
Kiến thức áp dụng
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Đúng 0
Bình luận (0)
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.Hình 29
Đọc tiếp
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
Hình 29
Cách 1: (Chứng minh trực tiếp)
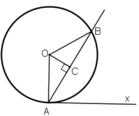
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
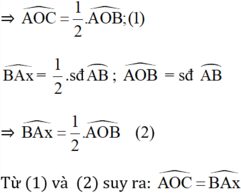
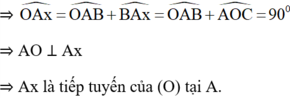
Cách 2: (Chứng minh phản chứng)
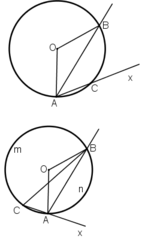
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB

+ C nằm trên cung lớn AB
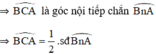
Mà 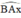 là góc ngoài của tam giác BAC
là góc ngoài của tam giác BAC
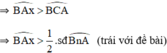
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.
Đúng 0
Bình luận (0)
Cho đường tròn (O), dây AB. Trên tia BA lấy điểm C sao cho A nằm giữa B và C. Từ điểm chính giữa P của cung lớn AB, kẻ đường kính PQ của đường tròn, cắt dây AB tại D. Tia CP cắt đường tròn (O) tại điểm thứ hai là I. Các dây AB và QI cắt nhau tại K.
a) Chứng minh: các điểm P, D, K, I cùng thuộc một đường tròn.
b) Chứng minh: CI.CP = CK.CD.
c) Chứng minh: KA.KB = CA.CB
Cho nửa đường tròn tâm O đường kính AB và dây CD. Độ dài dây CD không đổi. Chứng minh trung điểm I của CD thuộc một đường tròn cố định
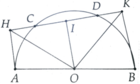
Ta có I thuộc đường tròn tâm O bán kính R = O A 2 - C D 2 4 = 1 2 4 O A 2 - C D 2
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
a) Hãy xác định vị trí tương đối của hai đường tròn.
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.
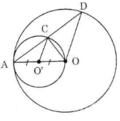
a) Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.
b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.
⇒ OC ⊥ AD
+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD
⇒ ΔAOD cân tại O mà OC ⊥ AD
⇒ OC là đường trung tuyến của ΔAOD
⇒ C là trung điểm của AD
⇒ AC = CD
Đúng 0
Bình luận (0)


