Ta có I thuộc đường tròn tâm O bán kính R = O A 2 - C D 2 4 = 1 2 4 O A 2 - C D 2

Ta có I thuộc đường tròn tâm O bán kính R = O A 2 - C D 2 4 = 1 2 4 O A 2 - C D 2
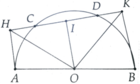
Cho nửa đường tròn (O) có đường kính AB = 2R. CD là dây cung thay đổi của nửa đường tròn sao cho CD = R và C thuộc cung AD (C khác A và D khác B). AD cắt BC tại H, hai đường thẳng AC và BD cắt nhau tại F.
c) Gọi I là trung diểm của HF. Chứng minh tia OI là tia phân giác của góc COD.
d) Chứng minh điểm I thuộc một đường tròn cố định khi CD thay đổi
Cho nửa đường tròn tâm O đường kính AB, dây CD có độ dài không đổi và khác AB. Gọi I là hình chiếu vuông góc của O trên CD; H,K theo thứ tự là hình chiếu vuông góc của A,B trên CD
a) Chứng minh I là trung điểm HK
b) Gọi E là hình chiếu vuông góc của I trên AB. Chứng minh rằng Sacb + Sadb = IE.AB
c) Tìm vị trí dây CD để diện tích AHKB lớn nhất
cứu mình với huuhhu
Cho nửa đường tròn tâm O, đường kính AB = 10 cm. Dây CD có hai điểm C và D thay đổi
trên đường tròn và độ dài không đổi bằng 8 cm. Gọi E và F lần lượt là hình chiếu vuông góc của A
và B trên CD.
a) Chứng minh
CE=BF .
b) Xác định vị trí của CD để diện tích tứ giác ABFE lớn nhất.
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
Bài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.
Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a) Tính khoảng cách từ tâm đến mỗi dây b) chứng minh rằng ba điểm B, O, C thẳng hàng.
Bài 4. Cho đường tròn (O), hai dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Trên tia đối của tia AB lấy điểm E sao cho AE = BM. Trên tia đối của tia CD lấy điểm F sao cho CF = DM. Chứng minh rằng OE = OF.
Bài 5. Cho đường tròn (O), hai dây AB và CD có AB > CD, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. So sánh các độ dài MH và MK.
giải giúp mình vs ạ . tạo mình đang cần gấp . cảm ơn nha
cho đường tròn (O) đường kính AB. Trên AB lấy điểm I sao cho OA= 3OI. Qua I vẽ dây CD vuông góc với AB. Trên CD lấy điểm K tùy ý, tia AK cắt đường tròn (O) tại điểm thứ hai là M
a) Chứng minh tứ giác IKMB nội tiếp
b) Chứng minh rằng tâm F của dường tròn ngoại tiếp tam giác MKC nằm trên một đường thẳng cố định
c) Khi K di chuyển trên CD, tính độ dài nhỏ nhất của DF
Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyên động trên cung lớn CD (E khác A). Nôi AE cắt CD tại K. Nối BE cắt CD tại H
a, Chứng minh bốn điểm B, M, E, K thuộc một đường tròn
b, Chứng minh AE.AK không đổi
c, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc A M B ^ không đổi
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC và diện tích hình viên phân giói hạn bởi dây AC và cung nhỏ AC
Cho ( O) đường kính CD , kẻ dây AB vuông góc với đường kính CD tại I ( I thuộc đoạn thẳng OC ) . Qua A kẻ AM vuông góc với BD ( M ∈ BD ) , cắt CD tại N.
a) Chứng minh: 4 điểm A, I, M, D cùng thuộc một đường tròn. Xác định tâm của đường tròn đó.
b) Chứng minh AC song song với BN.
c) Chứng minh IM là tiếp tuyến của đường tròn tâm K đường kính DN
Cho đường tròn (O; R), kính AB cố định. Gọi M là trung điểm của OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD. Nối AE cắt CD tại K. Nối BE cắt CD tại H.
a) C/m: AE.AK không đổi
b) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
c) C/m: tâm I của đường tròn ngoại tiếp tam giác BHK luôn thuộc một đường thẳng cố định.