Tìm đạo hàm của hàm số sau :
\(y=\dfrac{ax+b}{a+b}\)
SK
Những câu hỏi liên quan
Tìm đạo hàm của hàm số: y = a x + b a + b
Tìm đạo hàm của hàm số sau :
\(y=\left(a+\dfrac{b}{x}+\dfrac{c}{x^2}\right)^4\) (a, b, c là các hằng số)
JE
30 tháng 1 2021 lúc 23:11
cho hàm số \(y=\dfrac{3x^2+2x+1}{x-2}\) có đạo hàm là biểu thức có dạng \(\dfrac{ax^2+bx+c}{\left(2x-4\right)^2}\). tinh \(a^2-b^2+c^2\)
\(y'=\dfrac{\left(3x^2+2x+1\right)'\left(x-2\right)-\left(x-2\right)'\left(3x^2+2x+1\right)}{\left(x-2\right)^2}\)
\(y'=\dfrac{\left(6x+2\right)\left(x-2\right)-3x^2-2x-1}{\left(x-2\right)^2}\)
\(y'=\dfrac{6x^2-10x-4-3x^2-2x-1}{\left(x-2\right)^2}=\dfrac{3x^2-12x-5}{\left(x-2\right)^2}=\dfrac{12x^2-48x-20}{\left(2x-4\right)^2}\)
\(\Rightarrow a^2-b^2+c^2=12^2-48^2+20^2=...\)
Đúng 2
Bình luận (0)
Tìm đạo hàm của hàm số sau: y = (x - a)(x - b)
Tìm a,b để hàm số sau có đạo hàm trên R f(x)
x
2
-
x
+
1
khi
x
≤
1...
Đọc tiếp
Tìm a,b để hàm số sau có đạo hàm trên R
f(x)= x 2 - x + 1 khi x ≤ 1 - x 2 + ax + b khi x > 1
A. a=3; b=-1
B. a=3; b=-11
C. a=13;b=-1
D. a=23; b=-21
Tìm a; b để các hàm số sau có đạo hàm trên R.
f
x
x
2
-
x
+
1
k...
Đọc tiếp
Tìm a; b để các hàm số sau có đạo hàm trên R. f x = x 2 - x + 1 k h i x ≤ 1 - x 2 + a x + b k h i x > 1
A. a = 13 b = - 1
B. a = 3 b = - 11
C. a = 23 b = - 21
D. a = 3 b = - 1
JE
30 tháng 1 2021 lúc 23:03
Đạo hàm của hàm số \(y=\left(ax+b\right)sinx+\left(cx+d\right)cosx\). tinh \(a+b+2c+d\)?
Hở, là sao nhỉ? Đạo hàm xong nhưng tính a+b+2c+d kiểu gì?
Đúng 0
Bình luận (0)
Giúp mik với ạ
Xác định hàm số bậc nhất yax+b trong các trường hợp sau:
a)adfrac{4}{3}và dồ thị của hàm số cắt trục tung hoành tại điểm có hoành độ bằng dfrac{1}{3}
b)adfrac{2}{3}và dồ thị của hàm số đi qua điểm Aleft(-dfrac{1}{2};dfrac{3}{5}right)
c)Đồ thị của hàm số song song với đường thẳng ysqrt{3}xvà đi qua điểm Bleft(1;sqrt{3}+5right)
Đọc tiếp
Giúp mik với ạ
Xác định hàm số bậc nhất y=ax+b trong các trường hợp sau:
a)\(a=\dfrac{4}{3}\)và dồ thị của hàm số cắt trục tung hoành tại điểm có hoành độ bằng \(\dfrac{1}{3}\)
b)\(a=\dfrac{2}{3}\)và dồ thị của hàm số đi qua điểm A\(\left(-\dfrac{1}{2};\dfrac{3}{5}\right)\)
c)Đồ thị của hàm số song song với đường thẳng \(y=\sqrt{3}x\)và đi qua điểm B\(\left(1;\sqrt{3}+5\right)\)
a) Đồ thị hàm số cắt Ox tại điểm có hoành độ bằng \(\dfrac{1}{3}\) \(\Rightarrow x=\dfrac{1}{3};y=0\)
\(\Rightarrow\dfrac{4}{3}\cdot\dfrac{1}{3}+b=0\) \(\Rightarrow b=-\dfrac{4}{9}\)
Vậy \(y=\dfrac{4}{3}x-\dfrac{4}{9}\)
b) Đồ thị hàm số đi qua \(A\left(-\dfrac{1}{2};\dfrac{3}{5}\right)\) \(\Rightarrow x=-\dfrac{1}{2};y=\dfrac{3}{5}\)
\(\Rightarrow\dfrac{2}{3}\cdot\dfrac{-1}{2}+b=\dfrac{3}{5}\) \(\Rightarrow b=\dfrac{14}{15}\)
Vậy \(y=\dfrac{2}{3}x+\dfrac{14}{15}\)
c) Vì đồ thị hàm số song song với đường thẳng \(y=\sqrt{3}x\)
\(\Rightarrow\left\{{}\begin{matrix}a=\sqrt{3}\\b\ne0\end{matrix}\right.\) \(\Rightarrow y=\sqrt{3}x+b\)
Vì đồ thị hàm số đi qua \(B\left(1;\sqrt{3}+5\right)\)
\(\Rightarrow\sqrt{3}\cdot1+b=\sqrt{3}+5\) \(\Rightarrow b=5\)
Vậy \(y=\sqrt{3}x+5\)
Đúng 1
Bình luận (0)
Tìm a, b để các hàm số sau có đạo hàm trên R:
f
(
x
)
x
2
-
x
+
1
k
h
i
x
≤
1
-...
Đọc tiếp
Tìm a, b để các hàm số sau có đạo hàm trên R: f ( x ) = x 2 - x + 1 k h i x ≤ 1 - x 2 + a x + b k h i x > 1
A. a = 13 b = - 1
B. a = 3 b = - 11
C. a = 23 b = - 21
D. a = 3 b = - 1
- Với x ≠ 1 thì hàm số luôn có đạo hàm.
- Do đó hàm số có đạo hàm trên R khi và chỉ khi hàm số có đạo hàm tại x=1.
- Ta có:
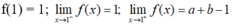
→ Hàm số liên tục trên R
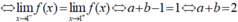
- Khi đó:
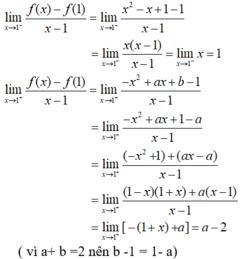
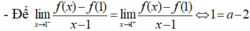
- Nên hàm số có đạo hàm trên R thì:
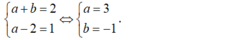
Chọn D
Đúng 0
Bình luận (0)