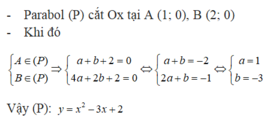Cho parabol ; y= -x2 và đường thẳng y=mx -1 . Tìm m để đường thẳng cắt parabol tại 2 điiểm có hoành độ x1 ,x2 thỏa mãn x12 x2 + x1x22 - x1x2 =3
DT
Những câu hỏi liên quan
Cho Parabol \(y=x^2\) . Tìm điểm A thuộc parabol sao cho tiếp tuyến với parabol tại A song song với đường thẳng y = 4x + 5
Gọi phương trình tiếp tuyến d tại A của parabol có dạng \(y=4x+b\) (\(b\ne5\))
Pt hoành độ giao điểm d và (P):
\(x^2=4x+b\Leftrightarrow x^2-4x-b=0\) (1)
d tiếp xúc (P) \(\Leftrightarrow\) (1) có nghiệm kép
\(\Leftrightarrow\Delta'=4+b=0\Rightarrow b=-4\)
Hoành độ giao điểm: \(x=\frac{4}{2.1}=2\Rightarrow y=4\Rightarrow A\left(2;4\right)\)
Đúng 0
Bình luận (0)
Câu T. Cho parabol (P): y= x +5x-6. Xác định trục đối xứng, tọa độ đinh của parabol (P), tọa độ giao điểm của parabol (P) với trục hoành.
Sửa đề: (P): \(y=x^2+5x-6\)
Tọa độ đỉnh của (P) là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=-\dfrac{5}{2}\\y=-\dfrac{\text{Δ}}{4a}=-\dfrac{5^2-4\cdot1\cdot\left(-6\right)}{4\cdot1}=-\dfrac{25+24}{4}=-\dfrac{49}{4}\end{matrix}\right.\)
=>Trục đối xứng của (P) là \(x=-\dfrac{5}{2}\)
Tọa độ giao điểm của (P) với trục Ox sẽ là nghiệm của hệ phương trình sau đây:
\(\left\{{}\begin{matrix}x^2+5x-6=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+6\right)\left(x-1\right)=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-6;1\right\}\\y=0\end{matrix}\right.\)
Vậy: Tọa độ các giao điểm của (P) với trục Ox là A(-6;0) và B(1;0)
Đúng 1
Bình luận (0)
Cho parabol y=ax^2 +bx +3
Xác định parabol ,biết rằng parabol đó đi qua A(-1,8) và B(0,3)
Cho parabol
y
1
4
x
2
. Xác định m để điểm A (
2
; m) nằm trên parabol A.
m
1
2
B.
m
−
1
2
C.
m
2
D.
m
−
2
Đọc tiếp
Cho parabol y = 1 4 x 2 . Xác định m để điểm A ( 2 ; m) nằm trên parabol
A. m = 1 2
B. m = − 1 2
C. m = 2
D. m = − 2
Thay x = 2 ; y = m vào hàm số y = 1 4 x 2
ta được m = 1 4 . 2 2 = 1 2
Vậy m = 1 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho Parabol P : y = 2 x 2 . Vẽ đồ thị parabol (P).
a) Vẽ Parabol P : y = 2 x 2
Bảng giá trị giữa x và y:
x |
-2 |
-1 |
0 |
1 |
2 |
y |
8 |
2 |
0 |
2 |
8 |
Vẽ đúng đồ thị
Đúng 0
Bình luận (0)
Cho parabol (P) có phương trình là y^2 = 16x tiêu điểm của parabol là
Cho Parabol y=1/4x2 . Xác định m để A(4; m) nằm trên parabol.
Do A nằm trên parabol thay tọa độ A vào pt parabol ra được:
\(\dfrac{1}{4}.4^2=m\)
\(\Rightarrow m=4\)
Đúng 0
Bình luận (0)
Cho parabol có phương trình \({y^2} = 8x\). Tìm tiêu điểm và đường chuẩn của parabol.
Ta có: \(2p = 8 \Rightarrow p = 4\) nên (P) có tiêu điểm là \(F\left( {2;0} \right)\) và đường chuẩn là \(x = - 2\).
Đúng 0
Bình luận (0)
Cho parabol (P): y a
x
2
+ bx + 2 biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ
x
1
1 và
x
2
2
x
2
2. Parabol đó là: A. y 12
x
2
+ x + 2. B. y −
x
2
+ 2x + 2. C. y 2...
Đọc tiếp
Cho parabol (P): y = a x 2 + bx + 2 biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ x 1 = 1 và x 2 = 2 x 2 = 2. Parabol đó là:
A. y = 12 x 2 + x + 2.
B. y = − x 2 + 2x + 2.
C. y = 2 x 2 + x + 2.
D. y = x 2 −3x + 2.
Trong mặt phẳng Oxy, cho parabol (P) : x2 - 4x + 9. Hỏi parabol nào sau đây là ảnh của parabol (P) qua phép đối xứng trục, có trục là đường thẳng x - 2 = 0
Parabol \(y=x^2-4x+9\) có trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}=2\)
Nên phép đối xứng trục qua đường thẳng \(x-2=0\) hay \(x=2\) sẽ cho ảnh là chính nó
Hay pt ảnh của (P) vẫn là \(x^2-4x+9\)
Đúng 1
Bình luận (0)