Khảo sát sự biến thiên của hàm sốy = x^2+2x-2 trên khoảng (-\(\infty\);-1)
và (-1; +\(\infty\)).
CH
Những câu hỏi liên quan
Một học sinh khảo sát sự biến thiên của hàm số như sau:I. Tập xác định:
D
ℝ
II. Sự biến thiên:
y
x
2
−
x
−
2
;
y
0
⇔
x
−
1
x...
Đọc tiếp
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
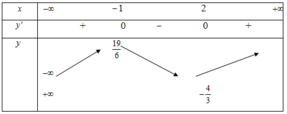
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Đáp án là D.
• Sai ở bước III (bảng biến thiên)
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và lập bảng biến thiên của hàm số :
y = x2 + 2x -2 trên ( -∞;1), (-1;+∞)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-x_2^2-2x_2+2}{x_1-x_2}\)
\(=\left(x_1+x_2\right)-2\)
Vì \(x_1;x_2\in\left(-\infty;1\right)\) thì \(\left\{{}\begin{matrix}x_1< 1\\x_2< 1\end{matrix}\right.\Leftrightarrow\left(x_1+x_2\right)< 2\)
\(\Leftrightarrow\left(x_1+x_2\right)-2< 0\)
Vậy: Hàm số nghịch biến trên \(\left(-\infty;1\right)\)
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên của hàm số sau:
y=\(x^2\)+2x-3
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = - x + 2 x + 2
y = - x + 2 x + 2
+) Tập xác định: D = R\{-2}
+) Ta có: 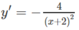
Bảng biến thiên:
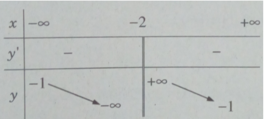
Hàm số nghịch biến trên các khoảng (− ∞ ; −2), (−2; + ∞ )
+) Tiệm cận đứng x = -2 vì
![]()
Tiệm cận ngang y = -1 vì
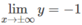
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
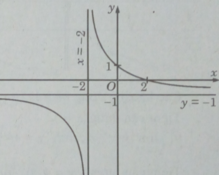
Đúng 0
Bình luận (0)
Cho hàm số y = x - 2 x + m - 1
Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số khi m = 2
Với m = 2 ta có hàm số 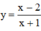
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
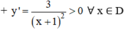
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
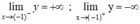
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
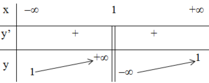
- Đồ thị :
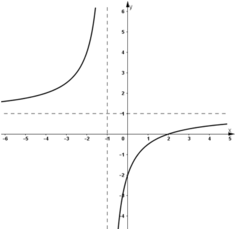
Đúng 0
Bình luận (0)
Khảo sat sự biến thiên của hàm số: y=\(\sqrt{x-4}\) + \(\sqrt{x+1}\) trên khoảng (4;\(+\infty\))
khảo sát sự biến thiên và vẽ đồ thị của hàm số sau:y=\(-x^2+2x-1\)
Khảo sát sự biến thiên của hàm số sau:
a;y=f(x)=\(\sqrt{x^2+2x+3}\)
b;y=f(x)=\(\sqrt{x^2-3x+2}\)
c;y=f(x)=\(\sqrt{-5x^2+2x+3}\)
Khảo sát sự biến thiên và vẽ đồ thị hàm số : \(y=-x^4+2x^2\)


