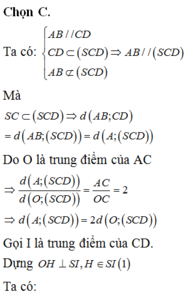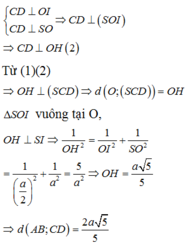Cho hình vuông ABCD có tâm O và cạnh bằng 3; M là trung điểm của cạnh CD. Khi đó độ dài của
ND
Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng 4cm và một hình tròn tâm O có đường kính bằng cạnh hình vuông. Hãy tính diện tích phần gạch chéo?
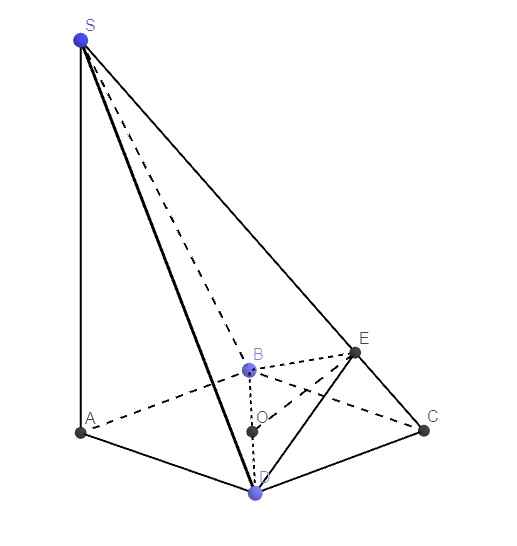
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. SO vuông góc (ABCD) và \(SO=\dfrac{a\sqrt{3}}{2}\). Tính \(\widehat{\left(SBC\right);\left(ABCD\right)}\)
Gọi E là trung điểm BC \(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}AB=\dfrac{a}{2}\\OE||AB\Rightarrow OE\perp BC\end{matrix}\right.\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SEO\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\Rightarrow\widehat{SEO}=60^0\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O có cạnh bằng a,SA=a√3 và SA vuông góc với (ABCD) a,CMR:DC vuông góc với (SAD) b, Tính góc giữa đường thẳng SD và mặt phẳng (ABCD)
a: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 3
=>góc SDA=60 độ
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có tâm O ,cạnh 2a. Trên đường thẳng qua O và vuông góc với mp (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng
45
0
. Độ dài SO bằng A.
S
O
a
2
B.
S
O
3
a
C.
S
O
...
Đọc tiếp
Cho hình vuông ABCD có tâm O ,cạnh 2a. Trên đường thẳng qua O và vuông góc với mp (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng 45 0 . Độ dài SO bằng
A. S O = a 2
B. S O = 3 a
C. S O = 3 2 a
D. S O = 2 2 a
Cho hình vuông ABCD có tâm O ,cạnh 2a. Trên đường thẳng qua O và vuông góc với mp(ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng
45
0
. Độ dài SO bằng: A.
S
O
2
a
B.
S
O
3
a
C.
S
O
3
2
a...
Đọc tiếp
Cho hình vuông ABCD có tâm O ,cạnh 2a. Trên đường thẳng qua O và vuông góc với mp(ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng 45 0 . Độ dài SO bằng:
A. S O = 2 a
B. S O = 3 a
C. S O = 3 2 a
D. S O = 2 2 a
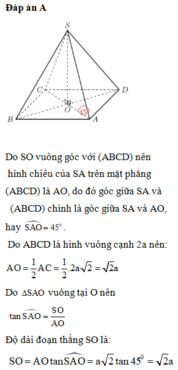
Đáp án A
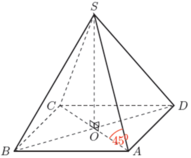
Do SO vuông góc với (ABCD) nên hình chiếu của SA trên mặt phẳng (ABCD) là AO, do đó góc giữa SA và (ABCD) chính là góc giữa SA và AO, hay S A O ^ = 45 0 . Do ABCD là hình vuông cạnh 2a nên: A O = 1 2 A C = 1 2 .2 a 2 = 2 a
Do Δ S A O vuông tại O nên tan S A O ^ = S O A O
Độ dài đoạn thẳng SO là: S O = A O tan S A O ^ = a 2 tan 45 0 = 2 a
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có tâm O, cạnh 2a. Trên đường thẳng qua O và vuông góc với mặt phẳng (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng
45
°
. Độ dài SO bằng: A.
S
O
a
2
B.
S
O
a
3
C.
S
O
a
3
2
D. ...
Đọc tiếp
Cho hình vuông ABCD có tâm O, cạnh 2a. Trên đường thẳng qua O và vuông góc với mặt phẳng (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) bằng 45 ° . Độ dài SO bằng:
A. S O = a 2
B. S O = a 3
C. S O = a 3 2
D. S O = a 2 2
Cho hình chóp .S ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và
S
O
a
. Khoảng cách giữa SC và AB bằng
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và S O = a . Khoảng cách giữa SC và AB bằng
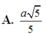
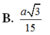
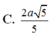
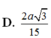
Cho hình chóp SABCD có đáy ABCD là hình vuông tâm O cạnh bằng a SA vuông góc với mặt phẳng ABCD SA = a căn 3 gọi alpha là mặt phẳng qua AB và vuông góc với SC T

\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)
Đúng 1
Bình luận (1)
Cho hình tròn tâm O và hình vuông ABCD có cạnh AB bằng 6cm tính diện tích?
Bán kính của hình tròn là:6:2=3[cm]
Diện tích hình tròn là:3x3x3,14=28,26[cm2]
Đáp số: 28,26 cm2
Đúng 0
Bình luận (0)
diện tích hình vuông là: 6x6=36 m2
vậy diện tích hình tròn là: 6:2x6:2x3,14= 9,42 m2
tổng diện tích là: 9,42+36= 45,42 m2
đ/s:...
k mk nhé, ko chắc đou nha
Đúng 0
Bình luận (0)
Diện tích hình vuông
6 x 6 = 36 ( cm2 )
Diện tích AOB
36 : 4 = 9 ( cm2 )
Diện tích .....
9 x 2 = 18 (cm2)
AO X OB chính là tích 2 bán kính diện tích của hình tròn
18 x 3,14 = 56,52 (cm2 )
Diện tích là
56,52 - 36 = 20,52 (cm2 )
ĐS: 20,52 cm2
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a√3 . O là tâm hình vuông . Chứng minh (SAC) vuông góc (ABCD) ; (SAC) vuông góc (SBD)
Do S.ABCD là chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\)
Mà \(O\in AC\Rightarrow SO\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
Đúng 0
Bình luận (0)