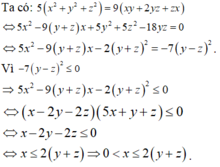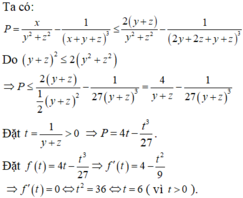Tìm các số nguyên dương thỏa mãn 1 + 4.3x + 4.3y = z2.
BT
Những câu hỏi liên quan
Cho các số x,y,z dương thỏa mãn:
x2 +y2 +z2 = 1. Tìm GTNN của M= 1/16x2 +1/4y2 + 1/z2
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{49}{16}\)
\(M_{min}=\dfrac{49}{16}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{\sqrt{7}};\dfrac{2}{\sqrt{14}};\dfrac{2}{\sqrt{7}}\right)\)
Đúng 1
Bình luận (1)
Cho các số x,y,z dương thỏa mãn:
x2 +y2 +z2 = 7/4. Tìm GTNN của M= 1/16x2 +1/4y2 + 1/z2
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{7}{4}\)
\(M_{min}=\dfrac{7}{4}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{\sqrt{2}};1\right)\)
Đúng 3
Bình luận (2)
Cho x là số thực dương thỏa mãn
3
2
x
+
3
4
.3
x
. Tính giá trị của
x
2
−
1
.
A. 0 B. 0 và -1 C. 0 và 1 D. 1
Đọc tiếp
Cho x là số thực dương thỏa mãn 3 2 x + 3 = 4 .3 x . Tính giá trị của x 2 − 1 .
A. 0
B. 0 và -1
C. 0 và 1
D. 1
Cho x là số thực dương thỏa mãn 3 2 x + 3 = 4 . 3 x . Tính giá trị của x 2 - 1
A. 0 và 1
B. 0
C. 0 và -1
D. 1
Cho hai số phức
z
1
,
z
2
thỏa mãn điều kiện
z
1
z
2
1
và
z
1
+
z
2
3
. Biết rằng , trong đó m, n,...
Đọc tiếp
Cho hai số phức z 1 , z 2 thỏa mãn điều kiện z 1 = z 2 = 1 và z 1 + z 2 = 3 . Biết rằng , trong đó m, n, p là các số nguyên dương và phân số m p tối giản. Tính S = 15 m + 12 n + 2019 p .
A. 2087
B. 4159
C. 6093
D. 4087
Chọn đáp án D.
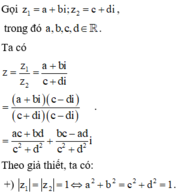
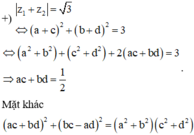
nên kết hợp với các đẳng thức ở trên, ta được

Tổng quát bài toán chúng ta có kết quả sau:
![]()
trong đó m, n, p là độ dài ba cạnh của một tam giác thì
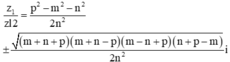
Đúng 0
Bình luận (0)
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)
Cho các số thực dương x, y, z thay đổi và thỏa mãn:
5
x
2
+
y
2
+
z
2
9
x
y
+
2
y...
Đọc tiếp
Cho các số thực dương x, y, z thay đổi và thỏa mãn: 5 x 2 + y 2 + z 2 = 9 x y + 2 y z + z x . Tìm giá trị lớn nhất của biểu thức: P = x y 2 + z 2 - 1 x + y + x 3 bằng
A. 18..
B. 12.
C. 16.
D. 24.
Trong tập các số phức gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
với
z
2
có phần ảo dương. Cho số phức z thỏa mãn |z-
z
1
| 1 Giá trị nhỏ nhất của P |z...
Đọc tiếp
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình 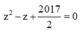
![]()
![]()
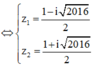
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Đúng 0
Bình luận (0)