Giá trị nhỏ nhất của là
0 câu trả lời
Toán lớp 8 Violympic toán 8Mình lớp 7, mình thi violympic toán lớp 7 mà như đang thi volympic toán lớp 8 vậy ak.
Nếu lớp 7 thì không cần phải tính giá trị nhỏ nhất hay giá trị lớn nhất rồi
:(
Nên mình đang ôn toán lớp 8 nên có gì mình không biết thì các bạn giúp mình nha!
mình thi toán volympic lớp 4 , mình hok lớp 4
k nha
Mình cũng thế nè
Mình cũng thế nè
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
BÀI 1: Điểm kiểm tra một tiết môn Toán của học sinh lớp 7A được ghi lại như sau:
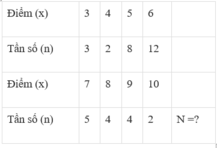
Giá trị có tần số nhỏ nhất là:
A. 3
B. 6
C. 9
D. 4
Chu vi của hình thang cân có độ dài cạnh bên là 7cm vàđộ dài đường trung bình là 14 cm.Vậy chu vi của hình thang cân đó là cm.
0 câu trả lời
Toán lớp 8 Violympic toán 8Xét đề bài với hình thang cân ABCD
Theo đề bài, ta có:
EF = \(\frac{AB+CD}{2}\) =14 => B + CD = 14 x 2 = 28 cm
Lại có: AD = BC = 7 cm
=> Chu vi hình thang cân ABCD là:
7 + 7 + 28 = 42 cm
hjhi, làm liền kẻo các bn làm trước
độ dài dg tb = 14cm nên tổng độ dài 2 đáy là: 14.2 = 28cm
chu vi hình thang cân là: 7.2 + 28 = 42cm
* Trả lời câu hỏi 6, 7, 8 với đề toán sau:
Điều tra về chiều cao của 100 học sinh khối lớp 11, ta có kết quả sau:
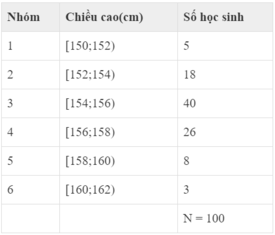
Giá trị đại diện của nhóm thứ 5 là:
A. 156,5
B. 158
C. 158,5
D. 159
Chọn D.
Nhóm thứ 5 là: [158;160)
Giá trị đại diện của nhóm thứ 5 là:
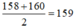
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
BÀI 2: Số điểm kiểm tra 15 phút môn Toán của một lớp 7 của một trường THCS được ghi lại trong bảng sau:
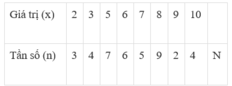
Phần trăm giá trị có tần số nhỏ nhất là:
A. 3%
B. 4%
C. 5%
D. 6%
**giúp mình với các bạn mình đang cần gấp***
toán cực trị lớp 8
cho a>0, b>0 và a+b = 3
a) tìm giá trị nhỏ nhất của N=a2+b2
b) tìm giá trị lớn nhất của P=ab+2
a)Áp dụng BĐT bunhiacoxki ta có: \(\left(a^2+b^2\right)\left(1^2+1^2\right)\ge\left(a.1+b.1\right)^2=\left(a+b\right)^2=3^2=9\)
=>\(2\left(a^2+b^2\right)\ge9\Leftrightarrow a^2+b^2\ge\frac{9}{2}\)
Dấu "=" xảy ra khi: a=b
Vậy GTNN của N là 9/2 tại a=b
b)Ta có: \(a^2+b^2\ge\frac{9}{2}\) (câu a)
<=>(a+b)2-2ab\(\ge\frac{9}{2}\)
<=>\(9-2ab\ge\frac{9}{2}\)
<=>\(2ab\le\frac{9}{2}\)
<=>\(ab\ge\frac{9}{4}\)
<=>\(ab+2\le\frac{17}{4}\)
Dấu "=" xảy ra khi a=b
Vậy GTLN của P là 17/4 tại a=b
help
Cho các số a; b; c thỏa mãn a + b + c ≠ 0 và ![]()
Khi đó giá trị của biểu thức: ![]() là: M = ...........
là: M = ...........
Ta có: \(\frac{a+b}{c}=\frac{b+c}{a}=\frac{c+a}{b}=\frac{2a+2b+2c}{a+b+c}=2\)
\(\Rightarrow\) a + b = 2c; b + c = 2a; c + a = 2b
\(\Rightarrow\) M = \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)\)
= \(\left(\frac{a+b}{b}\right)\left(\frac{b+c}{c}\right)\left(\frac{a+c}{a}\right)\)
= \(\frac{2c}{b}\times\frac{2a}{c}\times\frac{2b}{a}\)
= 8
Vậy: M = 8.
Tìm giá trị x>0
thỏa mãn \(\left|x-1\right|+\left|2x-6\right|=8\)
giúp với !!! violympic toán vòng 6 lớp 7 nhak
Câu 1: Số phần tử của tập hợp A = {0; 1; 2; 3; 4}
Câu 2: -25 = ...
Câu 3: Tổng các ước tự nhiên của số 24
Câu 4: -15 - ǀ-15ǀ = ...
Câu 5: Giá trị nhỏ nhất của C = ǀ2x + 22016ǀ + 5.102
Câu 6: BCNN (5; 13)
Câu 7: Số nhỏ nhất có dạng
Câu 8: ǀ25 - 2.52ǀ = ...
Câu 9: Giá trị nhỏ nhất của A = ǀx - 1ǀ - 25
Giải nha các bạn
Câu 1 : 5
Câu 2 : -32
Câu 3 : 60
Câu 4 : -30
Câu 5 : 500
Câu 6 : 65
Câu 7 : 50
Câu 8 : 25
Câu 9 : - 25
Câu 1: Tập hợp A có 5 phần tử
Câu 2: -2^5 = -32
Câu 3: Tổng các ước tự nhiên của 24 là 60
Câu 4: Kết quả là -30
Câu 5: Giá trị nhỏ nhất của C là 500
Câu 6: BCNN (5; 13) = 65
Câu 7: Số nhỏ nhất có dạng 5a là 50
Câu 8: Kết quả là 25
Câu 9: Giá trị nhỏ nhất của A là -25
Chúc bạn Bảo Bình love học tốt!