Mọi người giải giúp mình câu 8a với
PT
Những câu hỏi liên quan
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Đúng 0
Bình luận (0)
 Giúp mình giải câu h với mọi người ơi, lời giải chi tiết càng tốt ạ
Giúp mình giải câu h với mọi người ơi, lời giải chi tiết càng tốt ạ
Mình cảm ơn mọi người nhiều
Mình cần gấp í
Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
Đúng 0
Bình luận (0)
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2
Đúng 1
Bình luận (0)
Hộ mình với. Giải giúp mình cả câu 3 với câu 4
Cảm ơn mọi người
Mọi người giải quyết câu 4 giúp mình với nhanh giúp mình ạ 😓
mọi người giúp mình giải câu 4,5,6 với
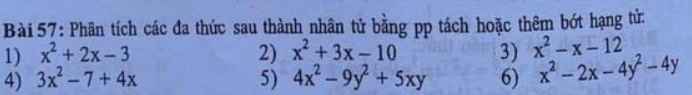
\(4,=3x^2-3x+7x-7=\left(x-1\right)\left(3x+7\right)\\ 5,=4x^2-4xy+9xy-9y^2=\left(x-y\right)\left(4x+9y\right)\\ 6,=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)=\left(x+2y\right)\left(x-2y-2\right)\)
Đúng 0
Bình luận (0)
1: \(x^2+2x-3=\left(x+3\right)\left(x-1\right)\)
2: \(x^2+3x-10=\left(x+5\right)\left(x-2\right)\)
3: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
4,=3x2−3x+7x−7=(x−1)(3x+7)
5,=4x2−4xy+9xy−9y2=(x−y)(4x+9y)
6,=(x−2y)(x+2y)−2(x+2y)=(x+2y)(x−2y−2)
Đúng 0
Bình luận (0)
mọi người ơi giải giúp mình câu này với 20 phút nữa mình kiểm tra rùi, cảm ơn mọi người nhiều
Đọc tiếp
mọi người ơi giải giúp mình câu này với 20 phút nữa mình kiểm tra rùi, cảm ơn mọi người nhiều
a. \(R=R1+R2+R3=5+6+15=26\Omega\)
b. \(I=I1=I2=I3=1A\left(R1ntR2ntR3\right)\)
\(\left\{{}\begin{matrix}U=IR=1.26=26\left(V\right)\\U1=I1.R1=1.5=5\left(V\right)\\U2=I2.R2=1.6=6\left(V\right)\\U3=I3.R3=1.15=15\left(V\right)\end{matrix}\right.\)
c. \(R'=U:I'=26:0,5=52\Omega\)
\(\Rightarrow R_x=R'-\left(R1+R2\right)=52-\left(5+6\right)=41\Omega\)
Đúng 5
Bình luận (0)
Mọi người giải giúp mình câu 238 với câu 239 vs ạ

mọi người giúp mình giải vài câu này với



Mọi người giải giúp mình câu b với ạ. 
Lời giải:
Vì $CF, BE$ là đường cao của tam giác $ABC$ nên:
$\widehat{AFH}=\widehat{AEH}=90^0$
Tứ giác $AEHF$ có tổng hai góc đối nhau $\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
b)
Vì $AFHE$ nội tiếp nên $\widehat{F_2}=\widehat{H_2}=\widehat{H_1}$
$\widehat{F_1}=\widehat{A_1}=90^0-\widehat{C}=\widehat{B_1}$
Áp dụng công thức $S_{ABC}=\frac{1}{2}.AB.AC\sin A$ ta có:
$\frac{HM}{AM}=\frac{S_{FMH}}{S_{AFM}}=\frac{FH.\sin F_1}{FA.\sin F_2}=\frac{FH}{FA}.\frac{\sin B_1}{\sin H_1}$
$=\tan A_2.\sin B_1.\frac{1}{\sin H_1}$
$=\frac{BK}{AK}.\frac{HK}{BH}.\frac{BH}{BK}$
$=\frac{HK}{AK}$
$\Rightarrow HM.AK=HK.AM$
Đúng 1
Bình luận (0)


