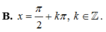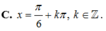2sin3x-sin2x+căn3 (2x)=0
H24
Những câu hỏi liên quan
y= (căn3).cos2x - sin2x + 2x.
Giải phương trình y'=0
\(y'=-2\sqrt{3}sin2x-2cos2x+2=0\)
\(\Leftrightarrow\sqrt{3}sin2x+cos2x=1\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x=\frac{1}{2}\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{6}\right)=sin\frac{\pi}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\2x+\frac{\pi}{6}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải phương trình
1,sin3x+cos2x=1+2sinx*cos2x
2,cos5x+cos2x+2sin3x*sin2x=0
căn3*cos3x + 2cos5x*sin2x + sin3x = 0
b. Cos3x - sin3x = - căn2
c. Căn3 sin2x + cos 2x =-căn 2
b.
\(\Leftrightarrow\sqrt{2}cos\left(3x+\frac{\pi}{4}\right)=-\sqrt{2}\)
\(\Leftrightarrow cos\left(3x+\frac{\pi}{4}\right)=-1\)
\(\Leftrightarrow3x+\frac{\pi}{4}=\pi+k2\pi\)
\(\Leftrightarrow x=...\)
c.
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{6}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{6}=-\frac{\pi}{4}+k2\pi\\2x+\frac{\pi}{6}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình lượng giác sau:
a) 2sin2x.cos2x+\(\sqrt{3}\)cos4x=\(-\sqrt{2}\)
b) \(sin2x+sin^2x=\frac{1}{2}\)
c) \(cos^2x-\sqrt{3}sin2x=1+sin^2x\)
d) \(5sin2x-6cos^2x=13\)
e) \(2sin3x+sin2x=\sqrt{3}cos2x\)
a.
\(sin4x+\sqrt{3}cos4x=-\sqrt{2}\)
\(\Leftrightarrow\frac{1}{2}sin4x+\frac{\sqrt{3}}{2}cos4x=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(4x+\frac{\pi}{3}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{\pi}{3}=-\frac{\pi}{4}+k2\pi\\4x+\frac{\pi}{3}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
\(2sin2x+2sin^2x=1\)
\(\Leftrightarrow2sin2x+1-cos2x=1\)
\(\Leftrightarrow2sin2x=cos2x\)
\(\Leftrightarrow tan2x=\frac{1}{2}\)
\(\Leftrightarrow2x=arctan\left(\frac{1}{2}\right)+k\pi\)
\(\Leftrightarrow...\)
c.
\(cos^2x-sin^2x-\sqrt{3}sin2x=1\)
\(\Leftrightarrow cos2x-\sqrt{3}sin2x=1\)
\(\Leftrightarrow\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x=\frac{1}{2}\)
\(\Leftrightarrow cos\left(2x+\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow...\)
d.
\(5sin2x-3\left(1+cos2x\right)=13\)
\(\Leftrightarrow5sin2x-3cos2x=16\)
Do \(5^2+\left(-3\right)^2< 16^2\) nên pt vô nghiệm
e.
\(\Leftrightarrow sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(3x-\frac{\pi}{2}\right)=cos\left(2x-\frac{\pi}{6}\right)\)
\(\Leftrightarrow...\)
giải các pt
a) \(\left(2sin^2x-1\right)tan^22x+3\left(2cos^2x-1\right)=0\)
b) \(tanx+tan2x=\frac{2sin3x}{sin2x}\)
c) \(1+sinx.cos2x=sinx+cos2x\)
d) \(tanx=1-cos2x\)
a/
DKXD: ...
\(\Leftrightarrow-cos2x.tan^22x+3.cos2x=0\)
\(\Leftrightarrow cos2x\left(3-tan^22x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\tan^22x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\tan2x=\sqrt{3}\\tan2x=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\2x=\frac{\pi}{3}+k\pi\\2x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{\pi}{6}+\frac{k\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/
DKXD: ...
\(\Leftrightarrow\frac{sinx}{cosx}+\frac{sin2x}{cos2x}-\frac{2sin3x}{sin2x}=0\)
\(\Leftrightarrow\frac{sinx.cos2x+sin2x.cosx}{cosx.cos2x}-\frac{2sin3x}{sin2x}=0\)
\(\Leftrightarrow\frac{sin\left(2x+x\right)}{cosx.cos2x}-\frac{2sin3x}{sin2x}=0\)
\(\Leftrightarrow\frac{sin3x}{cosx.cos2x}-\frac{2sin3x}{sin2x}=0\)
\(\Leftrightarrow sin3x\left(\frac{1}{cosx.cos2x}-\frac{2}{sin2x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin3x=0\left(1\right)\\2cosx.cos2x=sin2x\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow3sinx-4sin^3x=0\) (tìm nghiệm thẳng bằng \(3x=k\pi\) rồi dựa vào đường tròn lượng giác loại nghiệm cũng được)
\(\Leftrightarrow sinx\left(3-4sin^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\left(l\right)\\sinx=\pm\frac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\frac{\pi}{3}+k2\pi\\x=\frac{2\pi}{3}+k2\pi\\x=\frac{4\pi}{3}+k2\pi\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow2cosx.cos2x=2sinx.cosx\)
\(\Leftrightarrow2cosx\left(cos2x-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\left(l\right)\\cos2x=sinx=cos\left(\frac{\pi}{2}-x\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-x+k2\pi\\2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=-\frac{\pi}{2}+k2\pi\left(l\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow sinx.cos2x-sinx+1-cos2x=0\)
\(\Leftrightarrow sinx\left(cos2x-1\right)-\left(cos2x-1\right)=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\cos2x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Số nghiệm thuộc
π
7
;
56
π
13
của phương trình 2sin3x(1-4
sin
2
x
)1 là: A. 8. B. 12 C. 10 D. 24.
Đọc tiếp
Số nghiệm thuộc π 7 ; 56 π 13 của phương trình 2sin3x(1-4 sin 2 x )=1 là:
A. 8.
B. 12
C. 10
D. 24.
Đáp án D
Nhận thấy rằng cosx=0=>sinx=1 không là nghiệm của phương trình đã cho nên ta có:
![]()
![]()

Đúng 0
Bình luận (0)
Số nghiệm thuộc [
π
7
;
56
π
13
) của phương trình 2sin3x(1-4
sin
2
x
) 1 là: A. 8. B. 12. C. 10. D. 24.
Đọc tiếp
Số nghiệm thuộc [ π 7 ; 56 π 13 ) của phương trình 2sin3x(1-4 sin 2 x ) = 1 là:
A. 8.
B. 12.
C. 10.
D. 24.
Tìm nghiệm x của phương trình
2
sin
3
x
+
sin
2
x
-
sin
x
+
1
3
-
2
sin
x
-
cos
2
x
Đọc tiếp
Tìm nghiệm x của phương trình
2 sin 3 x + sin 2 x - sin x + 1 = 3 - 2 sin x - cos 2 x
![]()