Cho hai đa thức:
P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3;
Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b) Tính P(x) + Q(x) và P(x) - Q(x).
Cho hai đa thức:
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1.
Tính P(x) + Q(x) và P(x) – Q(x).
Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
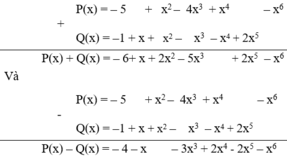
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6
Cho hai đa thức:
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1.
Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5
= – x6 + x4 – 4x3 + x2 – 5.
= – 5+ x2 – 4x3 + x4 – x6
Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1
= 2x5 – x4 + (x3 – 2x3) + x2 + x –1
= 2x5 – x4 – x3 + x2 + x –1.
= –1+ x + x2 – x3 – x4 + 2x5
Cho hai đa thức M(x)= 3x2 - 5 + x4 - 3x3 -x6 - 2x2 - x3
Và N(x)= x3 + 2x5 - x4 + x2 - 2x3 + x - 1
a, Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b, Tính M(x) + N(x) và M(x) - N(x).
c, Có thể chuyển phép trừ hai đa thức về phép cộng hai đa thức được không? Hãy thử tính M(x) - N(x) theo cách đó.
a) \(M\left(x\right)=-x^6+x^4-4x^3+x^2-5\)
\(N\left(x\right)=2x^5-x^4-x^3+x^2+x-1\)
b)\(M\left(x\right)+N\left(x\right)=-x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1\) \(=-x^6+2x^5-5x^3+2x^2+x-6\)
Vậy...
\(M\left(x\right)-N\left(x\right)=-x^6+x^4-4x^3+x^2-5-\left(2x^5+x^4-x^3+x^2-x-1\right)\)\(=-x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2+x+1\) \(=-x^6-2x^5+2x^4-3x^3+x-4\) Vậy...
c) -N(x)+M(x)=.........
Cho hai đa thức M(x)= 3x2 - 5 + x4 - 3x3 -x6 - 2x2 - x3
Và N(x)= x3 + 2x5 - x4 + x2 - 2x3 + x - 1
a, Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b, Tính M(x) + N(x) và M(x) - N(x).
c, Có thể chuyển phép trừ hai đa thức về phép cộng hai đa thức được không? Hãy thử tính M(x) - N(x) theo cách đó.
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
Cho hai đa thức M(x)= 3x2 - 5 + x4 - 3x3 -x6 - 2x2 - x3
Và N(x)= x3 + 2x5 - x4 + x2 - 2x3 + x - 1
a, Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b, Tính M(x) + N(x) và M(x) - N(x).
c, Có thể chuyển phép trừ hai đa thức về phép cộng hai đa thức được không? Hãy thử tính M(x) - N(x) theo cách đó.
giúp mk vs mk cần gấp
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
Cho hai đa thức M(x)= 3x2 - 5 + x4 - 3x3 -x6 - 2x2 - x3
Và N(x)= x3 + 2x5 - x4 + x2 - 2x3 + x - 1
a, Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
b, Tính M(x) + N(x) và M(x) - N(x).
c, Có thể chuyển phép trừ hai đa thức về phép cộng hai đa thức được không? Hãy thử tính M(x) - N(x) theo cách đó.
giúp mk vs mk cần gấp
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
Bài 1. Cho hai đa thức:
P(x) = 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6x
Q(x) = x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).
Bài 2. Cho hai đa thức:
P(x) = x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3
Q(x) = (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính P(x) + Q(x), P(x) - Q(x)
Bài 5. Cho hai đa thức:
P(x) = 2x4 + 2x3 - 3x2 + x +6
Q(x) = x4 - x3 - x2 + 2x + 1
a) Tính P(x) + Q(x), P(x) - Q(x)
b) Tính và P(x) - 2Q(x).
Bài 6. Cho đa thức P(x) = 2x4 - x2 +x - 2.
Tìm các đa thức Q(x), H(x), R(x) sao cho:
a) Q(x) + P(x) = 3x4 + x3 + 2x2 + x + 1
b) P(x) - H(x) = x4 - x3 + x2 - 2
c) R(x) - P(x) = 2x3 + x2 + 1
Bài 1: Giải phương trình:
a) ( x+1)2 (x+2) + ( x – 1)2 ( x- 2) = 12
b) x4 + 3x3 + 4x2 + 3x + 1 = 0
c) x5 – x4 + 3x3 + 3x2 –x + 1 = 0
Bài 2: Chứng minh rằng các phương trình sau vô nghiệm
a) x4 – x3 + 2x2 – x + 1 = 0
b) x4 + x3 + x2 + x + 1 = 0
c) x4 – 2x3 +4x2 – 3x +2 = 0
d) x6+ x5+ x4 + x3 + x2 + x + 1 = 0
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
2.
a. \(x^4-x^3+x^2+x^2-x+1=0\)
\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)
Vậy pt vô nghiệm
b.
\(x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)
Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)
Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn
Cho hai đa thức: A(x) = 3x3 – 2x2 + x + 1 + x4 và B(x) = 2x4 – x 3 – 5 + 3x2 – 4x a/ Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến. b/ Tính A(x) + B(x) và A(x) – B(x).
a: A(x)=x^4+3x^3-2x^2+x+1
B(x)=2x^4-x^3+3x^2-4x-5
b: A(x)+B(x)
=x^4+3x^3-2x^2+x+1+2x^4-x^3+3x^2-4x-5
=3x^4+2x^3+x^2-3x-4
A(x)-B(x)
=x^4+3x^3-2x^2+x+1-2x^4+x^3-3x^2+4x+5
=-x^4+4x^3-5x^2+5x+6
Bài 1: Phân tích các đa thức sau thành nhân tử
a)x2-y2-2x+2y e)x4+4y4
b)x2(x-1)+16(1-x) f)x4-13x2+36
c)x2+4x-y2+4 g) (x2+x)2+4x2+4x-12
d)x3-3x2-3x+1 h)x6+2x5+x4-2x3-2x2+1
a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$