giải pt: 2cos2x +sin2x -cos2x.cosx+1+sinx
NN
Những câu hỏi liên quan
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
1/ Tìm m để pt có nghiệm
|sinx+cosx| - sin2x=m
2/ Cho pt: 2cos2x+ sin2x.cosx + sinx.cos2x=m.(sinx + cosx)
A. Giải pt khi m=2
B. Tìm m để pt có nghiệm x thuộc [0; pi/2]
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
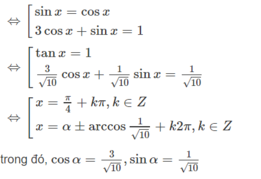
Đúng 0
Bình luận (0)
Giải pt sau:
A. (Sinx+1)(sinx-√2)=0
B.2sinxcosx=1
C. 4sinxcosxcos2x+1=0
D. Sin4x-cos4x=0
E. (Sinx+1)(2cos2x-√2)
F. Sin2x=cos4x/2-sin4x/2
d.
\(\Leftrightarrow\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=0\)
\(\Leftrightarrow sin^2x-cos^2x=0\)
\(\Leftrightarrow-cos2x=0\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
e. Đề thiếu
f.
\(\Leftrightarrow sin2x=\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)\left(cos^2\frac{x}{2}+sin^2\frac{x}{2}\right)\)
\(\Leftrightarrow sin2x=cos^2\frac{x}{2}-sin^2\frac{x}{2}\)
\(\Leftrightarrow sin2x=cosx\)
\(\Leftrightarrow sin2x=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-x+k2\pi\\2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a.
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\sqrt{2}>1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
b.
\(\Leftrightarrow sin2x=1\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
c.
\(\Leftrightarrow2sin2x.cos2x=-1\)
\(\Leftrightarrow sin4x=-1\)
\(\Leftrightarrow4x=-\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{\pi}{8}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
Giải pt (2cos2x-1)(sin2x+cos2x)=1
P/t \(\Leftrightarrow2cos2x.sin2x-sin2x+2cos^22x-cos2x-1=0\)
\(\Leftrightarrow sin4x-sin2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sinx.cos3x-2sin3x.sinx=0\)
\(\Leftrightarrow sinx\left(cos3x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\left(1\right)\\cos3x=sin3x\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow x=k\pi\left(k\in Z\right)\)
(2) \(\Leftrightarrow sin3x-cos3x=0\) \(\Leftrightarrow\sqrt{2}sin\left(3x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow3x-\dfrac{\pi}{4}=k\pi\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\left(k\in Z\right)\)
Vậy ...
Đúng 0
Bình luận (0)
Tìm nghiệm của phương trình
sin
2
x
+
2
cos
2
x
+
4
cos
x
−
sin
x
−
1
0
. A.
x
±
π
3
+
k
π
B.
x
±
π
3
+
k
2
π
C.
x...
Đọc tiếp
Tìm nghiệm của phương trình sin 2 x + 2 cos 2 x + 4 cos x − sin x − 1 = 0 .
A. x = ± π 3 + k π
B. x = ± π 3 + k 2 π
C. x = ± π 6 + k π
D. x = ± π 6 + k 2 π
Giải PT:
sin4x + 2cos2x + 4.(sinx + cosx) = 1 + cos4x
Lời giải:
PT $\Leftrightarrow 2\sin 2x\cos 2x+2\cos 2x+4(\sin x+\cos x)=1+\cos ^22x-\sin ^22x=2\cos ^22x$
$\Leftrightarrow \sin 2x\cos 2x+\cos 2x+2(\sin x+\cos x)=\cos ^22x$
$\Leftrightarrow \cos 2x(\sin 2x+1-\cos 2x)+2(\sin x+\cos x)=0$
$\Leftrightarrow \cos 2x(2\sin x\cos x+2\sin ^2x)+2(\sin x+\cos x)=0$
$\Leftrightarrow \cos 2x\sin x(\cos x+\sin x)+(\sin x+\cos x)=0$
$\Leftrightarrow (\sin x+\cos x)(\cos 2x\sin x+1)=0$
Nếu $\sin x+\cos x=0$. Kết hợp $\sin ^2x+\cos ^2x=1$ suy ra $(\sin x, \cos x)=(\frac{1}{\sqrt{2}}; \frac{-1}{\sqrt{2}})$ và hoán vị
$\Rightarrow x=k\pi -\frac{\pi}{4}$ với $k$ nguyên.
Nếu $\cos 2x\sin x+1=0$
$\Leftrightarrow (1-2\sin ^2x)\sin x+1=0$
$\Leftrightarrow (1-\sin x)(2\sin ^2x+2\sin x+1)=0$
$\Rightarrow \sin x=1$
$\Rightarrow x=2k\pi +\frac{\pi}{2}$ với $k$ nguyên.
Đúng 0
Bình luận (0)
Giải pt: 1/sinx + 1/sin2x + 1/sin4x =0
ĐKXĐ: \(\left\{{}\begin{matrix}sinx< >0\\sin2x< >0\\sin4x< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< >k\Omega\\2x< >k\Omega\\4x< >k\Omega\end{matrix}\right.\Leftrightarrow x\ne\dfrac{k\Omega}{4}\)
\(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}=0\)
=>\(\dfrac{1}{sinx}+cotx+\dfrac{1}{sin2x}+cot2x+\dfrac{1}{sin4x}+cot4x=cotx+cot2x+cot4x\)
=>\(\dfrac{1+cosx}{sinx}+\dfrac{1+cos2x}{sin2x}+\dfrac{1+cos4x}{sin4x}=cotx+cot2x+cot4x\)
=>\(\dfrac{2\cdot cos^2\left(\dfrac{x}{2}\right)}{2\cdot sin\left(\dfrac{x}{2}\right)\cdot cos\left(\dfrac{x}{2}\right)}+\dfrac{2\cdot cos^2x}{2\cdot sinx\cdot cosx}+\dfrac{2\cdot cos^22x}{2\cdot sin2x\cdot cos2x}=cotx+cot2x+cot4x\)
=>\(\dfrac{cos\left(\dfrac{x}{2}\right)}{sin\left(\dfrac{x}{2}\right)}+\dfrac{cosx}{sinx}+\dfrac{cos2x}{sin2x}=cotx+cot2x+cot4x\)
=>\(cot\left(\dfrac{x}{2}\right)+cotx+cot2x=cotx+cot2x+cot4x\)
=>\(cot4x=cot\left(\dfrac{x}{2}\right)\)
=>\(\left\{{}\begin{matrix}4x=\dfrac{x}{2}+k\Omega\\4x< >k\Omega\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{7}{2}x=k\Omega\\x< >\dfrac{k\Omega}{4}\end{matrix}\right.\Leftrightarrow x=\dfrac{2}{7}k\Omega\)
Đúng 0
Bình luận (0)
Giải pt: 1/sinx + 1/sin2x + 1/sin4x =0
\(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}=0\)
\(\dfrac{1}{sinx}+cotx+\dfrac{1}{sin2x}+cot2x+\dfrac{1}{sin4x}+cot4x=cotx+cot2x+cot4x\)
\(\dfrac{1+cosx}{sinx}+\dfrac{1+cos2x}{sin2x}+\dfrac{1+cos4x}{sin4x}=cotx+cot2x+cot4x\)
\(\dfrac{2cos^2\dfrac{x}{2}}{2sin\dfrac{x}{2}.cos\dfrac{x}{2}}+\dfrac{2cos^2x}{2sinx.cosx}+\dfrac{2cos^22x}{2sin2x.cos2x}=cotx+cot2x+cot4x\)
\(\dfrac{cos\dfrac{x}{2}}{sin\dfrac{x}{2}}+\dfrac{cosx}{sinx}+\dfrac{cos2x}{sin2x}=cotx+cot2x+cot4x\)
\(cot\dfrac{x}{2}+cotx+cot2x=cotx+cot2x+cot4x\)
\(cot\dfrac{x}{2}=cot4x\)
\(\Rightarrow\dfrac{x}{2}=4x+k\text{π}\)
\(\Leftrightarrow x=-\dfrac{k2\text{π}}{7}\)
Đúng 1
Bình luận (0)






