Giúp bài 2 với
PN
Những câu hỏi liên quan
giúp giúp mình bài 2 bài 3 với ạ
Đọc tiếp
giúp giúp mình bài 2 bài 3 với
ạ
2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Giúp mình 1 trong 2 bài này với ạ. Nếu được thì giải 2 bài này giúp mk với. Mình đang cần gấp lắm ạ 😢
jimmmmmmmmmmmmmmmmmmmmmmmmmmm
he he he he he he
bài 1:
bn lấy giá trị của √(4^2-3,9^2) là dc
bài 2
AB+BC=2√(3^2+4^2)=??
Xem thêm câu trả lời
giúp mình với ạ bài 1 với bài 2 ạ

Bài 2:
Ta có:\(2\sqrt{48}< 2\sqrt{49}\) ;
\(3\sqrt{27}>3\sqrt{25}\)
mà \(2\sqrt{49}< 3\sqrt{25}\left(14< 15\right)\)
\(\Rightarrow3\sqrt{27}>3\sqrt{25}>2\sqrt{49}>2\sqrt{48}\)
\(\Rightarrow3\sqrt{27}>2\sqrt{48}\)
b)
Ta có:\(\sqrt{50}+\sqrt{2}>\sqrt{49}+\sqrt{1}\)
\(\sqrt{50+2}< \sqrt{64}\)
mà \(\sqrt{49}+\sqrt{1}=\sqrt{64}\left(8=8\right)\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>8>\sqrt{50+2}\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>\sqrt{50+2}\)
Đúng 2
Bình luận (0)
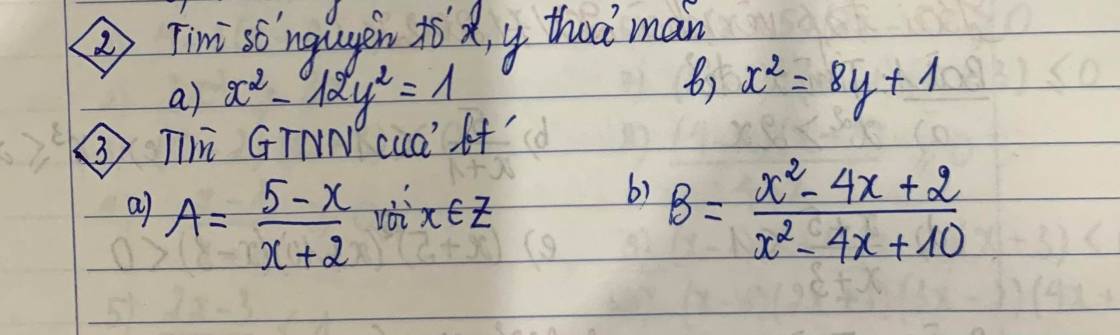 ai giúp em bài 2 với bài 3b với ạ
ai giúp em bài 2 với bài 3b với ạ
Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Đúng 0
Bình luận (0)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.
Đúng 0
Bình luận (0)
Bài 3:
a. $A=\frac{5-x}{x+2}=\frac{7-(x+2)}{x+2}=\frac{7}{x+2}-1$
Để $A$ min thì $\frac{7}{x+2}$ min
Điều này xảy ra khi $x+2$ là số nguyên âm lớn nhất
$\Rightarrow x+2=-1$
$\Rightarrow x=-3$. Khi đó: $A_{\min}=\frac{7}{-1}-1=-7-1=-8$
b.
$B=\frac{x^2-4x+10-8}{x^2-4x+10}=1-\frac{8}{x^2-4x+10}$
Để $B$ min thì $\frac{8}{x^2-4x+10}$ max
Điều này xảy ra khi $x^2-4x+10$ min
Mà: $x^2-4x+10=(x-2)^2+6\geq 6$ với mọi $x$
$\Rightarrow x^2-4x+10$ max = 6 khi $x=2$
Khi đó: $B_{\min}=1-\frac{8}{x^2-4x+10}=1-\frac{8}{2^2-4.2+10}=\frac{-1}{3}$
Đúng 0
Bình luận (0)
Giúp em nhanh với em cần gấp lắm bài 1b bài 2 với bài 3
Giúp em bài 1 hình 2 với bài 5 hình 4,6 với ạ.em cảm ơn anh chị và các bạn,mn giúp em giai chi tiết với ,để em áp dụng như vậy với nhìu bài sau

Bài 1: hình 2:
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow20x=144\Rightarrow x=\dfrac{36}{5}\)
\(x+y=BC\Rightarrow\dfrac{36}{5}+y=20\Rightarrow y=\dfrac{64}{5}\)
Bài 2:
hình 4:
BC=BH+HC=1+4=5
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow1.5=AB^2\Rightarrow x=\sqrt{5}\)
áp dụng HTL ta có: \(HC.BC=AC^2\Rightarrow4.5=AC^2\Rightarrow y=2\sqrt{5}\)
hình 6:
Áp dụng HTL ta có: \(BH.HC=AH^2\Rightarrow4x=25\Rightarrow x=\dfrac{25}{4}\)
Đúng 1
Bình luận (0)
GIÚP EM BÀI GIẢI PT VỚI TOÀN BỘ BÀI 2 VỚI Ạ
Mọi người giúp e làm bài 1 với bài 2 với ạ :((
2.a) = x^12 : x^6 = x^6
b) = (-x)^2=x^2
c) = 1/2.xy^3
d) -3/2.x^2.y
e) = (-xy)^7
f) = -4x^2 + 4xy - 6y^2
g) = xy - 2x + 4y
Đúng 0
Bình luận (0)
Bài 1:
a: A chia hết cho B
b: A chia hết cho B
c: A không chia hết cho B
d: A không chia hết cho B
Đúng 0
Bình luận (0)
Giúp mình với câu D, e, f bài 1 với bài 2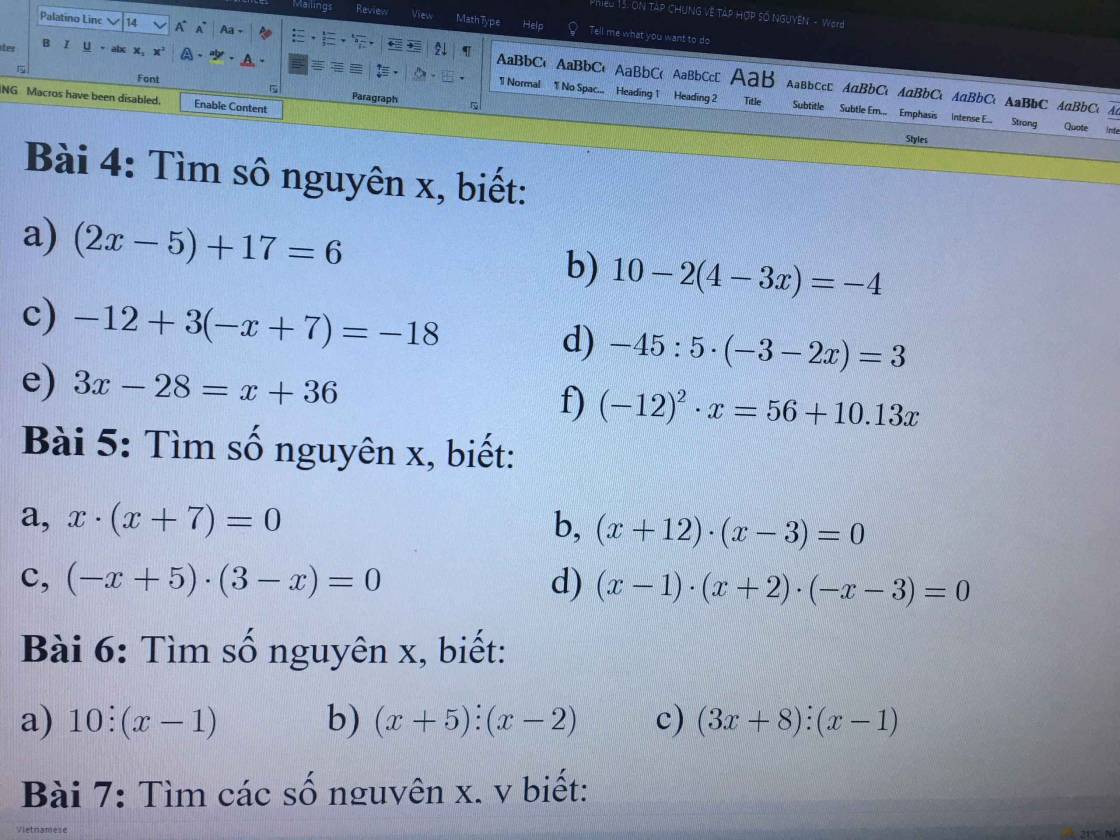
Xem thêm câu trả lời
Giúp mình bài 2 với bài 3
Bài 3:
a. \(\sqrt{9\left(x+3\right)}-\dfrac{1}{4}\sqrt{16\left(x+3\right)}+\sqrt{x+3}=6\)
\(\Leftrightarrow3\sqrt{x+3}-\sqrt{x+3}+\sqrt{x+3}=6\)
\(3\sqrt{x+3}=6\)
\(\sqrt{x+3}=2\)
\(\left\{{}\begin{matrix}2>0\left(ld\right)\\x+3=4\end{matrix}\right.\Leftrightarrow x=1\)
b. \(\sqrt{2x-1}=3\)
\(\left\{{}\begin{matrix}3>0\left(ld\right)\\2x-1=9\end{matrix}\right.\Leftrightarrow x=5\)
Đúng 2
Bình luận (1)
Bài 2:
\(a,B=\left[\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}+2\right]:\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-1\right]=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\\ b,B< 1\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-1}-1< 0\\ \Leftrightarrow\dfrac{\sqrt{x}+2-\sqrt{x}+1}{\sqrt{x}-1}< 0\\ \Leftrightarrow\dfrac{3}{\sqrt{x}-1}< 0\Leftrightarrow\sqrt{x}-1< 0\Leftrightarrow\sqrt{x}< 1\\ \Leftrightarrow0\le x< 1\)
Bài 3:
\(a,ĐK:x\ge-3\\ PT\Leftrightarrow3\sqrt{x+3}-\sqrt{x+3}+\sqrt{x+3}=6\\ \Leftrightarrow3\sqrt{x+3}=6\\ \Leftrightarrow\sqrt{x+3}=2\\ \Leftrightarrow x+3=4\\ \Leftrightarrow x=1\left(tm\right)\\ b,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow\sqrt{2x-1}=3\Leftrightarrow2x-1=9\\ \Leftrightarrow x=5\left(tm\right)\)
Đúng 2
Bình luận (1)








