Tìm m để hàm số \(y=\frac{mx^2-1}{x}\) có 2 điểm cực trị A,B và đoạn AB ngắn nhất
PH
Những câu hỏi liên quan
Cho y=\(\frac{1}{3}mx^3-\left(m-1\right)x^2-3\left(m-2\right)x+\frac{1}{3}\)
a. Tìm m để hàm số đồng biến trên R
b. Tìm m để hàm số nghịch biến trên R
c. Tìm m để hàm số có 2 cực trị
d. Tìm m để hàm số có 2 cực trị x1,x2 sao cho x1+3x2=1
e. Tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 1 (khi m>0)
Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^
Đúng 0
Bình luận (0)
Tìm tất cả giá trị thực của m để hàm số y=x^4-2(m^2-m+1)x^2+m-1 có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu là ngắn nhất.
Xem chi tiết
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).
Cho hàm số y = 2 x x - 1 (C). Giá trị m để hàm số y=mx=m+2 giao với (C) tại 2 điểm phân biệt A, B sao cho AB ngắn nhất là
A. m=1
B. m=2
C. m=3
D. m=4
Tìm m để hàm số y = \(\dfrac{-1}{3}x^{3} -2x^{2}+mx+3 \) có hai điểm cực trị A và B thỏa mãn
a) Đường thằng AB có hệ số góc k=2
b) Đường thẳng AB song song với đường thằng x+y-1=0
c) Đường thẳng AB vuông góc với đường thằng 3x+2y-3=0
Tìm m để hàm số \(f\left(x\right)=\frac{1}{3}x^3-mx^2-x+m+1\) có khoảng cách giữa các điểm cực đại và cực trị là nhỏ nhất.
Do \(f'\left(x\right)=x^2-2mx-1=0\)
Có \(\Delta'=m^2+1>0\) nên\(f'\left(x\right)=0\) có 2 nghiệm phân biệt \(x_1,x_2\) và hàm số đạt cực trị tại \(x_1,x_2\) với các điểm \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Thực hiện phép chia \(f\left(x\right)\) cho \(f'\left(x\right)\) ta có :
\(f\left(x\right)=\frac{1}{3}\left(x-m\right)f'\left(x\right)-\frac{2}{3}\left(m^1+1\right)x+\left(\frac{2}{3}m+1\right)\)
Do \(f'\left(x_1\right)=f\left(x_2\right)=0\) nên
\(y_1=f\left(x_1\right)=-\frac{2}{3}\left(m^1+1\right)x_1+\left(\frac{2}{3}m+1\right)\)
\(y_2=f\left(x_2\right)=-\frac{2}{3}\left(m^2+1\right)x_2+\left(\frac{2}{3}m+1\right)\)
Ta có \(AB^2=\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2=\left(x_2-x_1\right)^2+\frac{4}{9}\left(m^2+1\right)^2\left(x_2-x_1\right)^2\)
\(=\left[\left(x_2-x_1\right)^2-4x_2x_1\right]\left[1+\frac{4}{9}\left(m^2+1\right)^2\right]\)
\(=\left(4m^2+4\right)\left[1+\frac{4}{9}\left(m^2+1\right)^2\right]\ge4\left(1+\frac{4}{9}\right)\)
\(\Rightarrow AB\ge\frac{2\sqrt{13}}{3}\)
Vậy Min \(AB=\frac{2\sqrt{13}}{3}\) xảy ra <=> m=0
Đúng 0
Bình luận (0)
Tìm m để hàm số \(y=\frac{1}{3}x^3-mx^2+\left(2m-1\right)x+2\) có 2 điểm cực trị dương
Hàm số xác định trên R
Ta có \(y'=x^2-2mx+2m-1\Rightarrow y'=0\Leftrightarrow x^2-2mx+2m-1=0\left(2\right)\)
Hàm số có 2 điểm cực trị dương \(\Leftrightarrow\left(2\right)\) có 2 nghiệm dương phân biệt :
\(\Leftrightarrow\begin{cases}\Delta'=m^2-2m+1>0\\S=2m>0\\P=2m-1>0\end{cases}\) \(\Leftrightarrow\begin{cases}m>\frac{1}{2}\\m\ne1\end{cases}\)
Vậy \(\begin{cases}m>\frac{1}{2}\\m\ne1\end{cases}\) là giá trị cần tìm
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
x
2
+
m
x
-
2
có đồ thị (C). Tìm m để đồ thị (C) có hai điểm cực trị A, B và đường thẳng AB vuông góc với đường thẳng
d
:
y
1
2
x
+
1
A.
m
8
3
B. m 1 C.
m...
Đọc tiếp
Cho hàm số y = x 3 - x 2 + m x - 2 có đồ thị (C). Tìm m để đồ thị (C) có hai điểm cực trị A, B và đường thẳng AB vuông góc với đường thẳng d : y = 1 2 x + 1
A. m = 8 3
B. m = 1
C. m = - 8 3
D. m = - 26 3
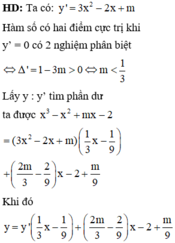
Phương trình đường thẳng đi qua 2 điểm cực trị là
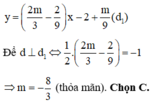
Đúng 0
Bình luận (0)
Cho hàm số y= mx^2 +2(m^2-5)x^4 +4 . Có bao nhiêu số nguyên m để hàm số có 3 điểm cực trị trong đó có đúng 2 điểm cực đại và 1 điểm cực tiểu.
Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn
Đúng 1
Bình luận (0)
1,Tìm tất cả các giá trị của m để hàm số y2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x2.
2, Tìm tất cả các giá trị của m để hàm số y x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x2.
3, Tìm tất cả các giá trị của m để hàm số yx^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu .
4, Tìm m để hso yx^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu.
Mọi người giúp em với ạ . Em cảm ơn ạ !
Đọc tiếp
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !


