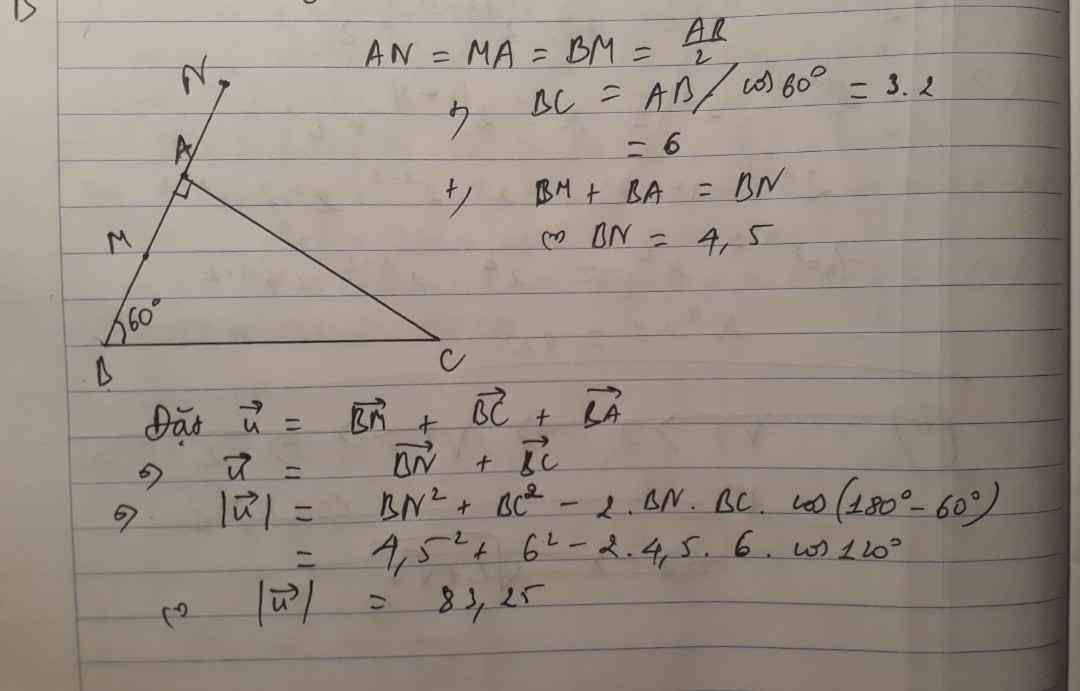Cho tam giác ABC vuông cân tại C, AB = 2a và I là trung điểm của BC. Tính |vecto AI - vecto IB|
DN
Những câu hỏi liên quan
Giúp tui :v
Bài 1 : Cho hình chữ nhật ABCD có AB = 2a,AD = a.Tính độ dài vecto AB + vecto DB
Bài 2 : Cho tam giác ABC gọi I là trung điểm trên cạnh BC sao cho 2CI=3BJ,J trên cạnh BC sao cho 5BJ=2CI.Phân tích vecto AI và AJ theo hai vecto AB,AC
Bài 1:
Gọi M là trung điểm của AD
\(BM=\sqrt{AB^2+AM^2}=\sqrt{4a^2+\dfrac{1}{4}a^2}=\dfrac{\sqrt{17}}{2}a\)
\(\left|\overrightarrow{AB}+\overrightarrow{DB}\right|=2\cdot BM=\sqrt{17}a\)
Đúng 2
Bình luận (0)
Câu 1: Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi Vecto IA + Vecto IB = ? giải thích tại sao
Câu 2: Điểm G là trọng điểm của tam giác ABC khi và chỉ khi vecto GA + vecto GB + vecto GC = ? giải thích
giúp mình 2 câu dưới với ạ
Câu 1: \(\overrightarrow{IA}+\overrightarrow{IB}=0\)
Bởi vì khi đó, IA và IB là hai vecto đối nhau
Suy ra: IA và IB là hai vecto cùng phương
mà IA và IB có điểm chung là I
nên A,I,B thẳng hàng và IA=IB
Suy ra: I là trung điểm của AB
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M, N, E lần lượt là trung điểm của AB, AC và BC. Gọi I là trung điểm của MN. Đặt vecto u vecto AB , vecto v vecto ACa) Hãy phân tích vecto AI theo hai vecto u và vb) Hãy phân tích vecto EI theo hai vecto u và v.
Đọc tiếp
Cho tam giác ABC. Gọi M, N, E lần lượt là trung điểm của AB, AC và BC. Gọi I là trung điểm của MN. Đặt vecto u = vecto AB , vecto v = vecto AC
a) Hãy phân tích vecto AI theo hai vecto u và v
b) Hãy phân tích vecto EI theo hai vecto u và v.
a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
Đúng 1
Bình luận (0)
Cho tam giác abc vuông tại b. AB=3a,BC=4a, vẽ điểm M sao cho Vecto MA+vecto MB-vecto MC=vecto 0,N là trung điểm của AC.Tính a dộ dài của vecto MN
Cho tam giác ABC. Gọi A’,B’, C’ lần lượt là trung điểm của BC, CA, AB. a) Chứng minh vecto AA’+ vecto BB’+ vecto CC’ = vecto 0 b) Đặt vecto BB’ = vecto u, CC’ = v. Tính vecto BC, CA, AB theo vecto u và v
a) ta có vector AA'+vectorBB'+vectorCC'=1/2(vectorAB+vectorAC+vectorBA+vectorBC+vectorCA+vectorCB)=vector 0
t/c trung tuyến
Đúng 0
Bình luận (0)
a.Hình chữ nhật ABCD. AB = 4a, BC = 2a, AC∩ BD = {O}. M là trung điểm CD
Tính tổng vecto AB+OM
b.Cho tam giác ABC đều. AB = a. M, N là trung điểm AC và AB. Tính tổng vecto CM +BN
Cho tam giác ABC vuông tại A có AB=3 góc B=60° .Gọi M là điểm thỏa vecto MA + vecto MB= vecto 0. Tính độ dài vecto BM + vecto BC + vecto BA
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
cho tam giác ABC cân tại A, có AB=6cm, BAC=120. Gọi M là trung điểm BC.chứng minh vectơ AB +vecto MC= vecto AC+ vecto MB / vecto AB- vecto CM/
Xem chi tiết
Sửa đề: Chứng minh \(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
\(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AM}\)
\(\overrightarrow{AC}-\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AC}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{MB}=\overrightarrow{AC}-\overrightarrow{MC}\)
=>\(\overrightarrow{AB}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{MB}\)
Đúng 0
Bình luận (0)