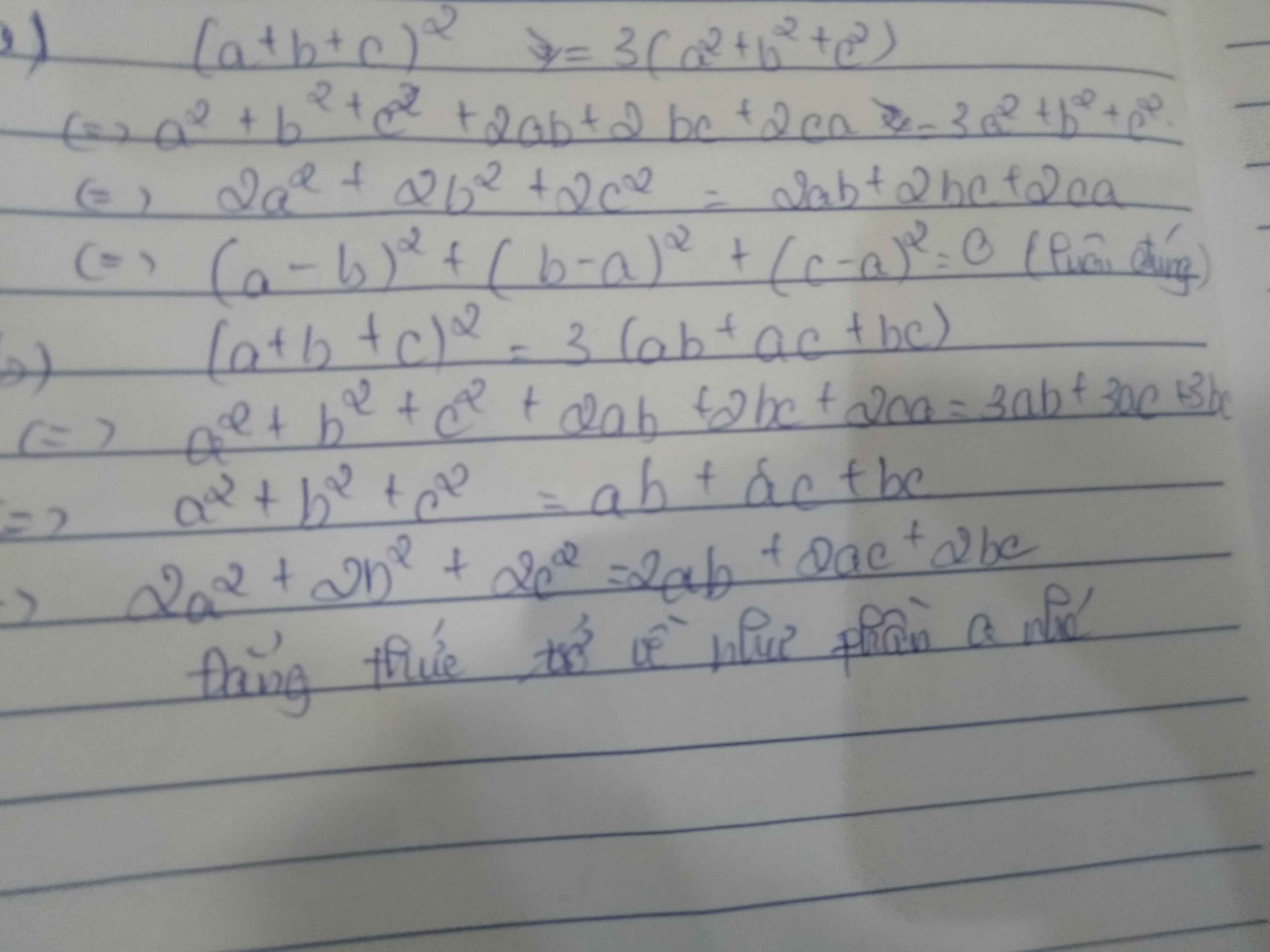1) Ta có: \(\left(a+b\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\cdot...\cdot\left(a^{32}+b^{32}\right)\)

\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\cdot...\cdot\left(a^{32}+b^{32}\right)\)

\(=\left(a^2-b^2\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\cdot...\cdot\left(a^{32}+b^{32}\right)\)

\(=\left(a^4-b^4\right)\left(a^4+b^4\right)\cdot...\cdot\left(a^{32}+b^{32}\right)\)

\(=\left(a^8-b^8\right)\left(a^8+b^8\right)\left(a^{16}+b^{16}\right)\left(a^{32}+b^{32}\right)\)

\(=\left(a^{16}-b^{16}\right)\left(a^{16}+b^{16}\right)\left(a^{32}+b^{32}\right)\)

\(=\left(a^{32}-b^{32}\right)\left(a^{32}+b^{32}\right)\)

\(=a^{64}-b^{64}\)

`1)(a+b+c)^2=3(a^2+b^2+c^2)`

`<=>a^2+b^2+c^2+2ab+2bc+2ca=3a^2+3b^2+3c^2`

`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`

`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`

`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`

Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`

Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`

`2)(a+b+c)^2=3(ab+bc+ca)`

`<=>a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca`

`<=>a^2+b^2+c^2=ab+bc+ca`

`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`

`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`

`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`

Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`

Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`

Vậy nếu `a=b=c` thì ....

1) Ta có: \(3\left(a^2+b^2+c^2\right)=\left(a+b+c\right)^2\)

\(\Leftrightarrow3a^2+3b^2+3c^2-a^2-b^2-c^2-2ab-2bc-2ac=0\)

\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(b^2-2bc+c^2\right)=0\)

\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=b\\a=c\\b=c\end{matrix}\right.\Leftrightarrow a=b=c\)

Ta có: a + b = 1 ⇔ b = 1 – a

Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:

a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2

⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1

⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)

Vậy bất đẳng thức được chứng minh

\(a+b=1=>b=1-a\)

\(=>a^2+\left(1-a\right)^2\ge\dfrac{1}{2}\)

\(=>a^2+1-2a+a^2\ge\dfrac{1}{2}\)

\(\Leftrightarrow-2a+2a^2+1\ge\dfrac{1}{2}\)

\(\Leftrightarrow\left(-2a+2a^2+1\right).2\ge1\)

\(\Leftrightarrow-4a+4a^2+2\ge1\)

\(\Leftrightarrow-4a+4a^2+1\ge0\)

\(\Leftrightarrow\left(2a-1\right)^2\ge0\left(đúng\right)\)

\(''=''\left(khi\right)2a-1=0=>a=\dfrac{1}{2}\)

Ta có: \(\left(a-b\right)^2\ge0\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow a^2+b^2\ge2ab\)

\(\Leftrightarrow a^2+b^2+a^2+b^2\ge2ab+a^2+b^2\)

\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)

\(\Leftrightarrow2\left(a^2+b^2\right)\ge1\)

\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(đpcm\right)\)

\(a+b=1\)

Áp dụng BĐT AM-GM, ta có:

\(\dfrac{a^2}{1}+\dfrac{b^2}{1}\ge\dfrac{\left(a+b\right)^2}{2}=\dfrac{1}{2}\) ( đpcm )

Đáp án A

86 vì ta học lớp 9

Ta có: \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)\)

\(=a\left(b^2c^2-b^2-c^2+1\right)+b\left(a^2c^2-a^2-c^2+1\right)\)

\(+c\left(a^2b^2-a^2-b^2+1\right)\)

\(=ab^2c^2-ab^2-ac^2+a+ba^2c^2-a^2b-bc^2+b\)

\(+ca^2b^2-a^2c-b^2c+c\)

\(=\left(ab^2c^2+ba^2c^2+ca^2b^2\right)+\left(a+b+c\right)\)

\(-\left(ab^2+ac^2+a^2b+bc^2+a^2c+b^2c\right)\)

\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)\)\(-\left[ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\right]\)

\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left[ab\left(a+b+c\right)+bc\left(a+b+c\right)+ca\left(a+b+c\right)\right]\)

\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left(a+b+c\right)\left(ab+bc+ca\right)\)

\(=abc\left(bc+ac+ab\right)+abc+3abc\)\(-abc\left(ab+bc+ca\right)=4abc\)

Vậy \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)=4abc\)(đpcm)

Với mọi số thực ta luôn có:

`(a-b)^2>=0`

`<=>a^2-2ab+b^2>=0`

`<=>a^2+b^2>=2ab`

`<=>2(a^2+b^2)>=(a+b)^2=1`

`<=>a^2+b^2>=1/2(đpcm)`

Dấu "=' `<=>a=b=1/2`

ta có:

(a²+b²)(1²+1²)≥(a.1+b.1)²

⇔ 2(a²+b²) ≥ (a+b)²

⇔ 2(a²+b²)≥ 1 (vì a+b=1)

⇔ a² +b² ≥ 1/2 (đpcm)

dấu "=) xảy ra khi a = b = 1/2

Ta có:

\(\dfrac{1}{a+b}+\dfrac{1}{b+c}\ge\dfrac{4}{a+2b+c}\ge\dfrac{4}{\dfrac{a^2+1}{2}+b^2+1+\dfrac{c^2+1}{2}}=\dfrac{8}{b^2+7}\)

Tương tự

\(\dfrac{1}{a+b}+\dfrac{1}{a+c}\ge\dfrac{8}{a^2+7}\)

\(\dfrac{1}{b+c}+\dfrac{1}{a+c}\ge\dfrac{8}{c^2+7}\)

Cộng vế:

\(2\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\ge\dfrac{8}{a^2+7}+\dfrac{8}{b^2+7}+\dfrac{8}{c^2+7}\)

\(\Rightarrow\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{4}{a^2+7}+\dfrac{4}{b^2+7}+\dfrac{4}{c^2+7}\)

Dấu "=" xảy ra khi \(a=b=c=1\)