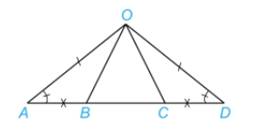
1. Cho 2 \(\Delta\)đều OAB & \(\Delta OA'B'\). Gọi C, D lần lượt là trung điểm của AA', BB'. CM \(\Delta OCD\) đều
2. Cho 2 \(\Delta\) vuông cân OAB và OA'B' chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đường thẳng A'B. Gọi G, G' lần lượt là trọng tâm \(\Delta OAA',\Delta OBB'\). CM \(\Delta GOG'\) vuông cân