Cho tam giác cân ABC có ∠A = 𝛼 (0 < a < 180). Tính số đo các góc còn lại.
H24
Những câu hỏi liên quan
Cho tam giác ABC cân tại A,biết B =50°.tính số đo các góc còn lại của tam giác đó
Xem chi tiết
Ta có tam giác ABC cân tại A
-> góc B = Góc C
mà góc B = 50 độ
-> góc C = 50 độ
Xét tam giác ABC có
góc A + góc B + góc C= 180 độ ( định lý tổng 3 góc trong tam giác)hay góc A + 50 + 50= 180 độ
góc A+ 100=180
góc A = 180-100
góc A = 80 độ
Đúng 1
Bình luận (0)
Xét tam giác ABC cân tại A có:
<B=<C=50 độ
=> <A= 180 độ -(<B+ <C)( Tổng 3 góc trong của tam giác)
=> <A= 180 độ -2.50 độ= 80 độ
P/S: cái "<" là chỉ góc nha bn
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Tính số đo các góc còn lại của tam giác ABC nếu biết:
a) A ^ = 40 °
b) B ^ = 50 °
c) C ^ = 60 °
Bài 1: Cho tam giác ABC cân tại A. Tính số đo các góc còn lại của tam giác ABC nếu biết: a) 40°; b) 50°; c) 60°.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A. Tính số đo các góc còn lại của tam giác ABC nếu biết:
a) ![]() = 40°; b)
= 40°; b) ![]() = 50°; c)
= 50°; c) ![]() = 60°.
= 60°.
Cho tam giác ABC cân tại A có AC=2 cm,góc B=45°.Tính độ dài cạnh AB và số đo các góc còn lại. Từ đó em cis nhận xét gì về tam giác ABC?
Help me!!!!
- Vì ∆ABC cân tại A, nên AB và AC là 2 cạnh bên
ð AB = AC = 2cm
- Vì ∆ABC cân tại A, nên góc B = góc C = 45 độ (2 góc đáy của một tam giac)
Ta có : góc A + góc B + góc C = 180 độ (tổng 3 góc trong một tam giac)
Góc A + 45 độ + 45 độ = 180 độ
ð Góc A = 180 độ - 45 độ - 45 độ
ð Góc A = 90
Nhận xét về ∆ABC :
Tam giác ∆ABC là tam giác vuông (vuông và cân tại A)
Đúng 2
Bình luận (0)
Cho tam giac ABC co góc A=75 độ.Lấy điểm D trên cạnh BC sao cho các tam giác ABD và tam giác ACD là tam giác cân. Tính số đo @ góc còn lại của tam giác ABC
Cho tam giác ABC có góc A = 75 độ. Lấy điểm D trên cạnh BC sao cho tam giác ABD và tam giác ACD là tam giác cân. Tính số đo 2 góc còn lại của tam giác ABC.
Tam giác ABC có số đo các góc A, B, C tỉ lệ 3 : 5 : 7. Tính số đo các góc của tam giác ABC (Biết rằng tổng số đo ba góc trong một tam giác bằng \(180^0\))
Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)
\(\Rightarrow\widehat{A}=12^o.3=36^o\)
\(\widehat{B}=12^o.5=60^o\)
\(\widehat{C}=12^o.7=84^o\)
Đúng 0
Bình luận (0)
nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)
vậy : A = 3 . 12 = 36
B = 5 . 12 = 60
C = 7 . 12 = 84
=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)
Đúng 0
Bình luận (0)
Gọi số đo của các góc A,B,C trong tam giác ABC lần lượt là là a,b,c
Ta có: \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và tổng ba góc là 180o
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{180^o}{15}=12^o\)
+) Nếu \(\dfrac{a}{3}=12\)⇒ a= 36o
+)Nếu \(\dfrac{b}{5}\)=12⇒b=60o
+)Nếu \(\dfrac{c}{7}\)=12⇒c=84o
Vậy góc A bằng 36o, góc B bằng 60o, góc C bằng 84o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có góc
A
^
110
°
. Đường trung trực của các cạnh AB và AC cắt nhau tại I. Chứng minh:a) tam giác BIC cân;b)
B
I
C
^
2
(
180
°
-
B
A
C
^
)
và...
Đọc tiếp
Cho tam giác ABC có góc A ^ = 110 ° . Đường trung trực của các cạnh AB và AC cắt nhau tại I. Chứng minh:
a) tam giác BIC cân;
b) B I C ^ = 2 ( 180 ° - B A C ^ ) và tính số đo góc B I C ^ .
Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Hai đường cao BD và CE cắt nhau tại H.
a) Tính số đo các góc còn lại của tam giác ABC.
b) Chứng minh BD = CE.
c) Chứng minh tia AH là tia phân giác của góc BAC.
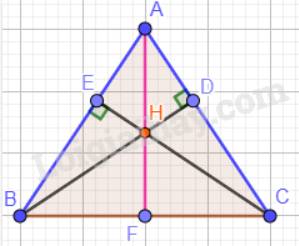
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.
Đúng 0
Bình luận (0)