Giải phương trình:
a,\(1+2Sinx=2Cosx\)
b,\(4Cosx-3Sinx=3\)
c,\(3Cos3x+4Sin3x=5\)
Giải phương trình 4 sin 3 x + 3 cos 3 x - 3 sin x - sin 2 x cos x = 0
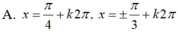
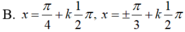
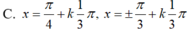
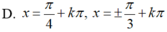
Giải phương trình:
a, 2sin2x - cos2x = 7sinx + 2cosx - 4
b, sin2x - cos2x + 3sinx - cosx -1 = 0
c, sin2x - 2cos2x + 3sinx - 4cosx + 1 = 0
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
Giải các phương trình :
a, 3sinx -2cosx =2
b, cosx +4sinx=-1
c, \(\sqrt{3}cosx+4sinx-\sqrt{3}\)=0
d, 2sinx-5cosx=5
a/
\(\Leftrightarrow\frac{3}{\sqrt{13}}sinx-\frac{2}{\sqrt{13}}cosx=\frac{2}{\sqrt{13}}\)
Đặt \(cosa=\frac{3}{\sqrt{13}}\) với \(0< a< \pi\)
\(\Rightarrow sinx.cosa-cosx.sina=sina\)
\(\Leftrightarrow sin\left(x-a\right)=sina\)
\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=\pi-a+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow cosx.\frac{1}{\sqrt{17}}+sinx.\frac{4}{\sqrt{17}}=-\frac{1}{\sqrt{17}}\)
Đặt \(cosa=\frac{1}{\sqrt{17}}\) với \(0< a< \pi\)
\(\Rightarrow cosx.cosa+sinx.sina=-cosa\)
\(\Leftrightarrow cos\left(x-a\right)=cos\left(\pi-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-a=\pi-a+k2\pi\\x-a=a-\pi+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=2a-\pi+k2\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow\frac{\sqrt{3}}{\sqrt{19}}cosx+\frac{4}{\sqrt{19}}sinx=\frac{\sqrt{3}}{\sqrt{19}}\)
Đặt \(cosa=\frac{\sqrt{3}}{\sqrt{19}}\) với \(0< a< \pi\)
\(\Rightarrow cosx.cosa+sinx.sina=cosa\)
\(\Leftrightarrow cos\left(x-a\right)=cosa\)
\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=-a+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=k2\pi\end{matrix}\right.\)
Giải các pt lượng giác sau:
a, 4cosx - 3sinx = √5.sin2x + √10
b, 4cosx - 3sinx = √5.sin2x
c, 4cosx - 3sinx = -5
Mn giúp mình vs ạ :3
Giải các phương trình sau:
a, \(\sqrt{2}\) sin \(\left(2x+\frac{\pi}{4}\right)\)=3sinx+cosx+2
b, 1+sinx+cosx+sin2x+cos2x=0
c, (2cosx-1)(2sinx+cosx)=sin2x-sinx
d, cos3x+cos2x-cosx-1=0
a.
\(\Leftrightarrow sin2x+cos2x=3sinx+cosx+2\)
\(\Leftrightarrow2sinx.cosx-3sinx+2cos^2x-cosx-3=0=0\)
\(\Leftrightarrow sinx\left(2cosx-3\right)+\left(cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left(sinx+cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=-1\\2cosx-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\\cosx=\frac{3}{2}\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
\(\Leftrightarrow1+sinx+cosx+2sinx.cosx+2cos^2x-1=0\)
\(\Leftrightarrow sinx\left(2cosx+1\right)+cosx\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)=2sinx.cosx-sinx\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)-sinx\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx-sinx\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx-1=0\\sinx+cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\sin\left(x+\frac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow...\)
(2sinx+cosx)(sinx+cosx) =3sinx +2cosx
Giải phương trình: 3sinx - 4cosx = 1
3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
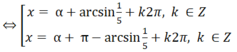
Giải phương trình sau giúp mình: 3sinx+4cosx=5+(4tanx-3)^2
ĐKXĐ; ...
\(\Leftrightarrow\frac{3}{5}sinx+\frac{4}{5}cosx-1=\frac{1}{5}\left(4tanx-3\right)^2\)
\(\Leftrightarrow sin\left(x+a\right)-1=\frac{1}{5}\left(4tanx-3\right)^2\)
(Trong đó \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{3}{5}\))
Do \(\left\{{}\begin{matrix}sin\left(x+a\right)-1\le0\\\left(4tanx-3\right)^2\ge0\end{matrix}\right.\) \(\forall a;x\) nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sin\left(x+a\right)=1\\4tanx-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3sinx+4cosx=5\\4sinx-3cosx=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sinx=\frac{3}{5}\\cosx=\frac{4}{5}\end{matrix}\right.\) \(\Rightarrow x=arcsin\left(\frac{3}{5}\right)+k2\pi\)
Giải các phương trình g ' ( x ) = 0 v ớ i g ( x ) = sin 3 x - 3 cos 3 x + 3 cos x - 3 sin x