3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
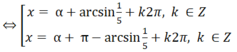
3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
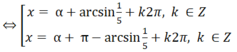
Giải phương trình:
a, 2sin2x - cos2x = 7sinx + 2cosx - 4
b, sin2x - cos2x + 3sinx - cosx -1 = 0
c, sin2x - 2cos2x + 3sinx - 4cosx + 1 = 0
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m ≤ 0
Tìm m để các bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≥ 2 m - 1 đúng với mọi x ∈ ℝ
A. m> 0
B. m ≤ 0
C. m < 0
D. m ≤ 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y= 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
![]()
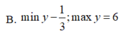
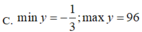
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 sin x + 4 cos x ) 2 + 4 ( 3 sin x + 4 cos x ) + 1
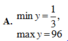
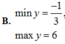
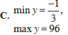
![]()
3sinx-4cosx=-5
Giải phương trình sau: 3 sin 2 x + 4 cos x - 2 = 0
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sinx+4cosx+1
![]()
![]()

![]()
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3 sin x + 4 cos x + 1
![]()
![]()
![]()
![]()